在 快速傅里叶变换中，单位复根用于多项式的分治过程，作为变量 $x$ 的取值。然而，使用单位复根有几个缺点：

1. 单位复根定义在三角函数之上：$${\omega }_N=\cos \frac{2\pi }{N}+i\sin \frac{2\pi }{N}$$在运算过程中，会频繁地跟浮点复数 complex<double> 打交道，导致精度损失；
2. 不适用于模环境（复数无法取模）；
3. 算法常数较大，影响效率。

幸运的是，在整数域中，我们找到了可替代单位复根的数值，它们仅在模环境中有效。这就是快速数论变换（Fast Number-Theoretic Transform, FNTT）的核心。

原根

对于质数 $p$，如果存在整数 $g$ 使

$$g^{0}modp,g^{1}modp,g^{2}modp,\cdots ,g^{p-2}modp$$

这 $p-1$ 个数互不相同，则称 $g$ 是 $p$ 的原根。

---

根据费马小定理：

对任意质数 $p\in \mathbb{P}$ 和任意整数 $a\in \mathbb{Z}$，都有 $a^{p-1}\equiv 1(\mathrm{mod}p)$。

因此 $g^{p-1}\equiv 1=g^0(\mathrm{mod}p)$。进一步地：

$$\begin{array}{r}{g}^p\equiv g^1(\mathrm{mod}p)\\ g^{p+1}\equiv g^2(\mathrm{mod}p)\\ g^{p+2}\equiv g^3(\mathrm{mod}p)\end{array}$$

这意味着，计算 $g$ 的更高幂次会重复之前的模 $p$ 序列，形成一个轮回。

我们可以将此轮回用环状结构表示。

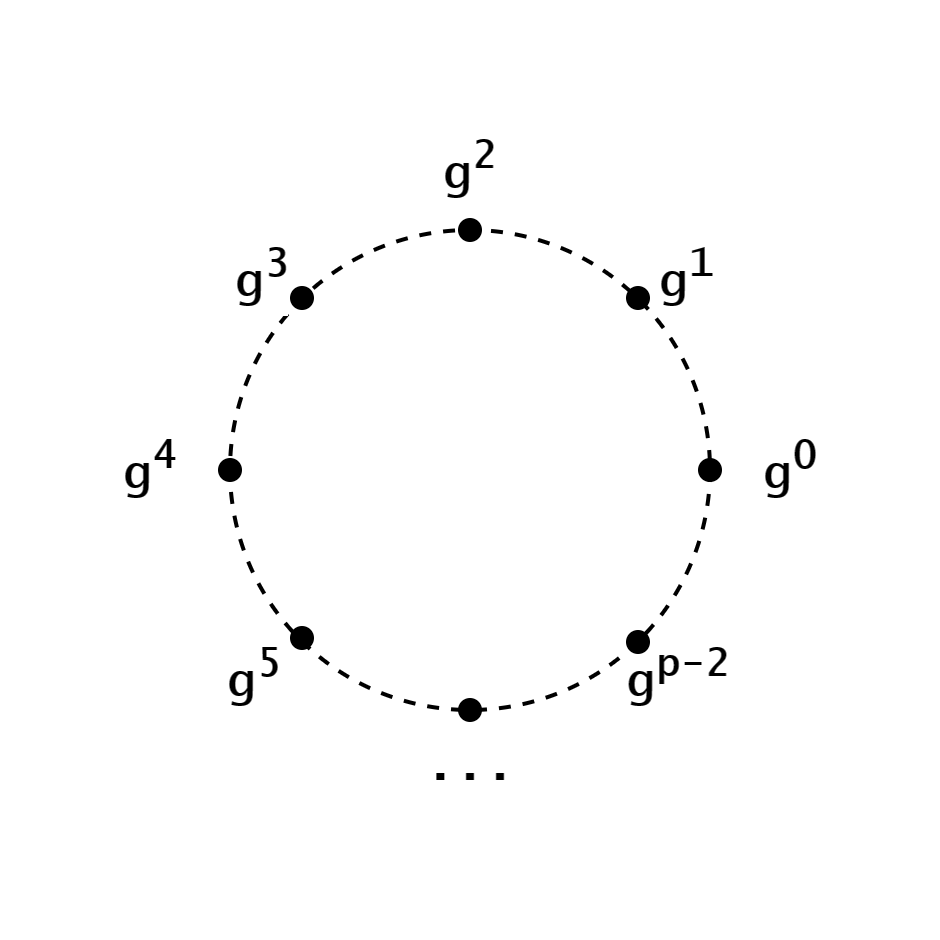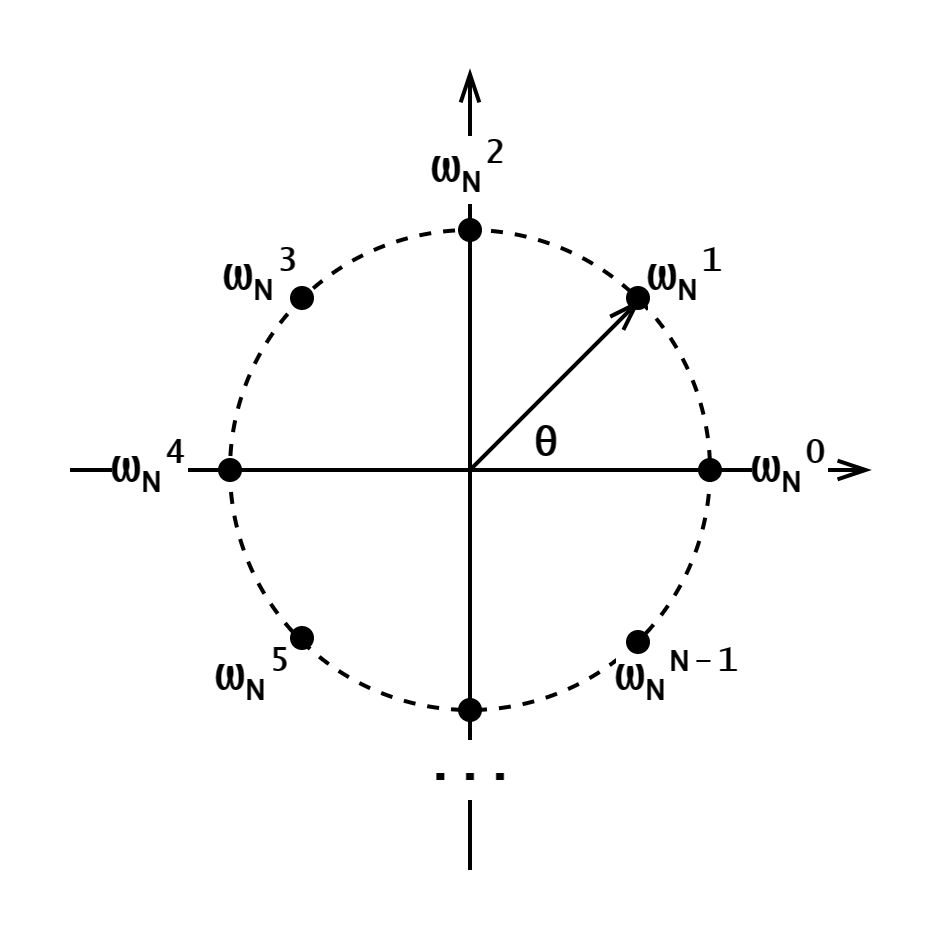模意义下原根的轮回	单位复根的轮回

是不是跟单位复根如出一辙。

基于原根的该性质，我们可以构造与单位复根同构的表达式。

现对质数 $p$ 作进一步的约束：令 $p$ 满足 $p=1+N$ 的形式，其中 $N=2^{\xi }$ 是 $2$ 的幂次。从而构造

$$G_N=g^{\frac{p-1}{N}}modp$$

可以发现，$G_N$ 具有单位复根 ${\omega }_N$ 的所有性质：

1. 周期性：$G_N^N=1$；

   证明：$G_N^N=g^{p-1}modp=1$。

2. 消去性：$G_{2N}^{2k}=G_N^k$；

   证明：$G_{2N}^{2k}=g^{\frac{p-1}{2N}\cdot 2k}modp=g^{\frac{p-1}{N}\cdot k}modp=G_N^k$。

3. 对称性：$G_N^{k+N/2}=-G_N^k$；

   证明：

   $$G_N^{k+N/2}=g^{\frac{p-1}{N}(k+\frac{N}{2})}modp=g^{\frac{p-1}{N}\cdot k}\cdot g^{\frac{p-1}{2}}modp=G_N^k\cdot g^{\frac{p-1}{2}}modp$$

   由于 ${\left(g^{\frac{p-1}{2}}\right)}^2=g^{p-1}\equiv 1(\mathrm{mod}p)$，故 $g^{\frac{p-1}{2}}\equiv \pm 1(\mathrm{mod}p)$。

   根据原根的定义，$g^0,g^1,\cdots ,g^{p-2}$ 在模 $p$ 意义下互不相同，因此 $g^{\frac{p-1}{2}}\not\equiv g^0=1(\mathrm{mod}p)$，即 $g^{\frac{p-1}{2}}modp$ 只能是 $-1$。代入得 $G_N^{k+N/2}=-G_N^k$。

因此 $G_N$ 可以完全替代单位复根，参与 FFT 的运算过程。

原根表

质数 $p$	原根 $g$	质数 $p$	原根 $g$
3	2	12289	11
5	2	40961	3
17	3	65537	3
97	5	786433	10
193	5	5767169	3
257	3	7340033	3
7681	17	23068673	3
104857601	3	167772161	3
469762049	3	998244353	3
1004535809	3	2013265921	31
2281701377	3	3221225473	5
75161927681	3	77309411329	7
206158430209	22	2061584302081	7
2748779069441	3	6597069766657	5
39582418599937	5	79164837199873	5
263882790666241	7	1231453023109120	3
1337006139375610	3	3799912185593850	5
4222124650659840	19	7881299347898360	6
31525197391593400	3	180143985094819000	6
1945555039024050000	5	4179340454199820000	3

注：一个质数可能对应多个原根。例如 $998244353$ 的原根可以是 $3$，也可以是 $114514$。

模板

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;

const LL Mod = 998244353;
const LL G = 114514;
const LL Gi = 137043501;

LL powmod(LL a, LL b) {
    LL res = 1;
    a %= Mod;
    while (b > 0) {
        if (b % 2 == 1)
            res = res * a % Mod;
        a = a * a % Mod;
        b /= 2;
    }
    return res;
}

vector<LL> NTT(vector<LL> a, bool invert) {
    int n = a.size();
    if (n == 1) return a;

    vector<LL> a0(n / 2), a1(n / 2);
    for (int i = 0; i < n / 2; i ++) {
        a0[i] = a[2 * i];
        a1[i] = a[2 * i + 1];
    }

    vector<LL> y0 = NTT(a0, invert);
    vector<LL> y1 = NTT(a1, invert);
    vector<LL> y(n);

    LL w = 1;
    LL root = powmod(!invert ? Gi : G, (Mod - 1) / n);

    for (int i = 0; i < n / 2; i ++) {
        LL u = y0[i];
        LL v = y1[i] * w % Mod;
        y[i] = (u + v) % Mod;
        y[i + n / 2] = (u - v + Mod) % Mod;
        w = w * root % Mod;
    }

    return y;
}

vector<LL> multiply(vector<LL> A, vector<LL> B) {
    int n = 1;
    while (n < A.size() + B.size()) 
        n *= 2;

    A.resize(n);
    B.resize(n);

    vector<LL> yA = NTT(A, false);
    vector<LL> yB = NTT(B, false);
    vector<LL> yC(n);

    for (int i = 0; i < n; i ++)
        yC[i] = yA[i] * yB[i] % Mod;

    vector<LL> C = NTT(yC, true);

    LL inv_n = powmod(n, Mod - 2);
    for (LL &x : C)
        x = x * inv_n % Mod;

    while (C.size() && ! C.back())
        C.pop_back();

    return C;
}

int main() {
    vector<LL> A = {1, 2, 3};
    vector<LL> B = {4, 5, 6};

    vector<LL> res = multiply(A, B);

    for (LL x : res)
        cout << x << " ";
    cout << endl;

    return 0;
}