简介

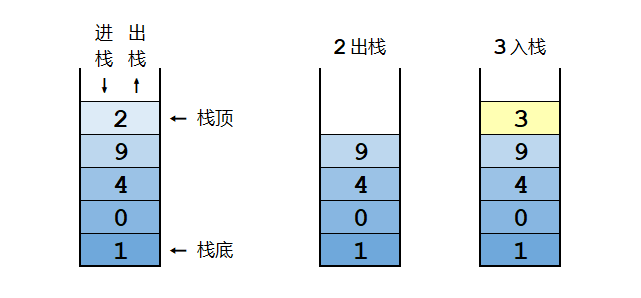
栈是一种「先进后出」的数据结构。类似于在桶中堆积物品，取物品时只能从顶端开始取，最先进桶的被压在最底下，最后被取出来。

表达式计算

算术表达式分为三类（$op$ 为运算符，$A,B$ 为数字或表达式）：

1. 中缀表达式：形如「$AopB$」，如「$5\times (3+2)$」；
2. 前缀表达式：形如「$opAB$」，如「$\times 5+32$」；
3. 后缀表达式：形如「$ABop$」，如「$32+5\times$」.

计算前/后缀表达式时，先递归求出 $A,B$ 的值，二者再做 $op$ 运算。计算方案是唯一确定的，且不需要使用括号。计算后缀表达式的算法最容易设计。

后缀表达式

1. 定义一个栈，用于存放数；
2. 逐一扫描后缀表达式中的元素：
   • 若扫到一个数 $n$，则把 $n$ 入栈；
   • 若扫到运算符 $op$ ，则弹出栈顶的两个元素，二者做 $op$ 计算。将计算结果入栈。

最终的栈顶元素就是计算结果。时间复杂度为 $O(n)$。

bool isdigit(char ch) { // 判断是否为数字
    return ch >= '0' && ch <= '9';
}

bool isop(char ch) { // 判断是否为运算符
    return ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^';
}

double postfix_calc(string str) {
    stack<double> s; int i = 0;
    s = stack<double>(); 
    while (i < str.size()) {
        if (isdigit(str[i])) { // 假定输入数据只包含整数
            double x = 0;
            while (isdigit(str[i]))
                x = x * 10 + str[i ++] - '0';
            s.push(x);
            continue;
        }
        else if (isop(str[i])) {
            double r = s.top(); s.pop();
            double l = s.top(); s.pop();
            double ans;
            switch (str[i]) {
                case '+' : ans = l + r; break;
                case '-' : ans = l - r; break;
                case '*' : ans = l * r; break;
                case '/' : ans = l / r; break;
                case '^' : ans = pow(l, r); break;
            }
            s.push(ans);
        }
        i ++;
    }
    return s.top();
}

中缀表达式

先将中缀表达式转换成 后缀表达式 再计算。

1. 定义一个栈，用于存放运算符；
2. 逐一扫描中缀表达式中的元素：
   • 若扫到一个数 $n$，直接输出 $n$；
   • 若扫到「左括号」，把左括号入栈；
   • 若扫到「右括号」，重复取栈顶并输出，直到栈顶为左括号。最后弹出左括号；
   • 若扫到其它运算符 $op$，重复取栈顶并输出，直到栈顶的优先级大于 $op$ 或者栈空。最后把 $op$ 入栈。

运算符优先级越大，越晚出栈，因此可以将「左括号」的优先级视作最低，「右括号」的优先级视作最高.

时间复杂度为 $O(n)$.

运算符	$($	$+/-$	$\times /÷$	$\wedge$	$)$
优先级	最低（0）	低（1）	中（2）	高（3）	最高（4）

int lev(char ch) { // 返回运算符对应的优先级 
    int level;
    switch (ch) {
        case '(' : level = 0; break; case ')' : level = 4; break;
        case '+' : level = 1; break; case '-' : level = 1; break;
        case '*' : level = 2; break; case '/' : level = 2; break;
        case '^' : level = 3; break;
    }
    return level;
}
    
double infix_calc(string str) {
    string data;
    stack<char> op;
    int i = 0;
    while (i < str.size()) {
        if (isdigit(str[i])) {
            while (isdigit(str[i]))
                data += str[i ++];
            data += ' '; // 数与数之间用空格区分
            continue;
        }
        else if (isop(str[i])) {
            while (!op.empty() && lev(op.top()) <= lev(str[i])) {
                if (op.top() != '(' && op.top() != ')')
                    data += op.top();
                op.pop();
            }
            op.push(str[i]);
        }
        i ++;
    }
    while (!op.empty()) { // 输出栈内剩余元素
        if (op.top() != '(' && op.top() != ')')
            data += op.top();
        op.pop();
    }
    return postfix_calc(data);
}

单调栈

单调栈中的元素从栈底到栈顶满足单调性。

插入元素

将元素 $x$ 入栈，同时维护栈的单调性。以单调递增栈为例：

• 从栈顶依次弹掉比 $x$ 大的元素，保证 $x\ge$ 栈顶；
• 将 $x$ 入栈。

stack<int> s;

void insert(int x) {
    while (!s.empty() && s.top() > x)
        s.pop();
    s.push(x);
}

应用

单调递增栈可以实现快速查询「左边第一个更小的元素」。例如 $A=\{1,2,5,4,3,6\}$，$A_5=3$ 的左边第一个比它小的元素是 $A_2=2$。

顺序扫描 $A$。将 $A_i$ 插入单调栈前，栈中比 $A_i$ 大的元素都被弹掉了，栈顶元素即为左边第一个比 $A_i$ 小的元素。

stack<int> s;

for (int i = 1; i <= n; i ++) {
    while (!s.empty() && s.top() > a[i])
        s.pop();
    if (!s.empty())
        cout << s.top() << endl; // 输出 a[i] 左边第一个更小的元素
    else cout << "none" << endl; // 如果没有则输出 none
    s.push(a[i]);
}

INFO

• 求左边第一个更小的元素：顺序扫描 + 单调递增栈；
• 求左边第一个更大的元素：顺序扫描 + 单调递减栈；
• 求右边第一个更小的元素：倒序扫描 + 单调递增栈；
• 求右边第一个更大的元素：倒序扫描 + 单调递减栈。