问题

数组 $A$ 中共 $n$ 个元素，对其反复进行以下操作共 $m$ 次：

• 单点修改：将 $A[id]$ 修改为 $v$；
• 区间查询：查询 $A[l\cdots r]$ 的最小值；
• 区间修改：将 $A[l\cdots r]$ 每个数加上 $v$。

int a[];

// 单点修改
void set(int id, int v) {
    a[id] = v;
}

// 区间查询
int ask(int l, int r) {
    int ans = 0;
    for (int i = l; i <= r; i ++)
        ans = min(ans, a[i]);
    return ans;
}

// 区间修改
void add(int l, int r, int v) {
    for (int i = l; i <= r; i ++)
        a[i] += v;
}

暴力算法（$\times$）	线段树（$\surd$）
单点修改	$O(1)$	$O(\log n)$
区间查询	$O(n)$	$O(\log n)$
区间修改	$O(n)$	$O(\log n)$
$m$ 次操作	$O(mn)$	$O(m\log n)$

构造

查询数组 $A=$$\{6,2,3,7,1,5,4,2\}$ 中的最小值时，可以使用「两两比较法」：每次比较相邻两项，只保留更小的一项。比较的过程可以画成一棵二叉树，树根是答案。

graph TD
A((6))
B((2))
C((3))
D((7))
E((1))
F((5))
G((4))
H((2))
I((2)) --> A
I --> B
J((3)) --> C
J --> D
K((1)) --> E
K --> F
L((2)) --> G
L --> H
M((2)) --> I
M --> J
N((1)) --> K
N --> L
O((1)) --> M
O --> N

这么做有什么好处呢？假如 $1$ 被改为 $7$，通过修改极少的数值，就能重新得出正确答案。

graph TD
A((6))
B((2))
C((3))
D((7))
E((7))
F((5))
G((4))
H((2))
I((2)) --> A
I --> B
J((3)) --> C
J --> D
K((5)) --> E
K --> F
L((2)) --> G
L --> H
M((2)) --> I
M --> J
N((2)) --> K
N --> L
O((2)) --> M
O --> N
classDef red fill:#fff3c2, stroke:#e57d21;
class E,K,N,O red;

线段树就是这样的一颗二叉树，它的每个节点都代表一段区间中的最小值。

线段树具有以下性质：

• 根节点的值为 $t[1]$，代表整个数组的最小值；
• $t[u]$ 的左子节点为 $t[2u]$，右子节点为 $t[2u+$$1]$；
• $t[u]=$$min\{t[2u],t[2u+1]\}$。

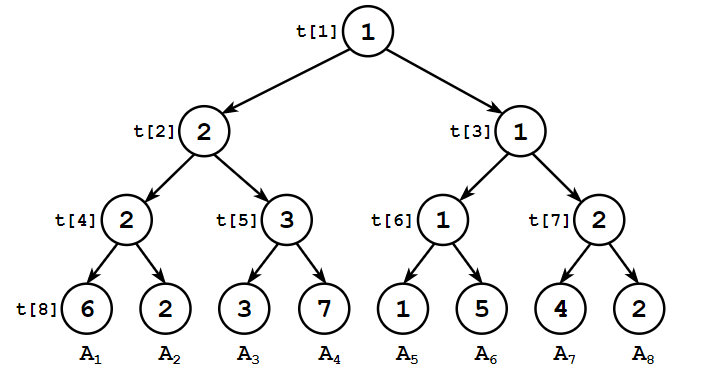
因此，每个节点需要保存以下信息：

• 节点的值：$val$；
• 节点代表的区间：$[l,$$r]$。

从根节点开始，自顶向下递归构建线段树。时间复杂度为 $O(n\log n)$。

struct Node {
    int val, l, r;
    #define t(u) t[u].val
    #define l(u) t[u].l
    #define r(u) t[u].r
} t[];

void build(int u, int l, int r) {
    l(u) = l, r(u) = r;
    if (l == r) { // 当前节点为叶节点
        t(u) = a[l]; return;
    }
    int m = (l + r) / 2;
    build(2 * u, l, m);         // 递归构建左子树
    build(2 * u + 1, m + 1, r); // 递归构建右子树
    t(u) = min(t(2 * u), t(2 * u + 1));
}

单点修改

假设你要将 $A[5]$ 修改为 $3$，则 $A[5]$ 的所有祖先都有可能变动。

$set(u,$$id,$$v)$：在以节点 $u$ 为根的子树中，找到 $A[id]$，并将其更新为 $v$。

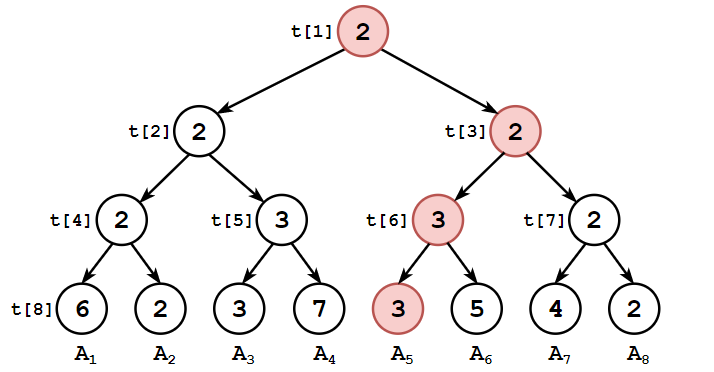
1. 令 ${\displaystyle m=}$$\frac{l(u)+r(u)}{2}$；
2. 若 $id\le m$，则 $A[id]$ 在左子树中，搜索左子树；
3. 若 $id>m$，则 $A[id]$ 在右子树中，搜索右子树；
4. 更新当前节点值：$t[u]=$$min\{t[2u],t[2u+1]\}$。

时间复杂度为 $O(\log n)$。

根节点是搜索的入口。执行 $set(1,$$id,$$v)$ 以进行单点修改。

void set(int u, int id, int v) { // 将 a[id] 改为 v
    if (l(u) == r(u)) { // 叶节点
        a[id] = t(u) = v; return;
    }
    int m = (l(u) + r(u)) / 2;
    if (id <= m) set(2 * u, id, v); // 搜索左子树
    else set(2 * u + 1, id, v);    // 搜索右子树
    t(u) = min(t(2 * u), t(2 * u + 1));
}

区间查询

线段树中，每个节点代表一个区间，每个区间都可通过若干节点实现完全覆盖。

例如 $A[1]\cdots A[6]$ 可以被 $t[2]$ 和 $t[6]$ 完全覆盖，那么有

$$min\{A[1]\cdots A[6]\}=min\{t[2],t[6]\}=2$$

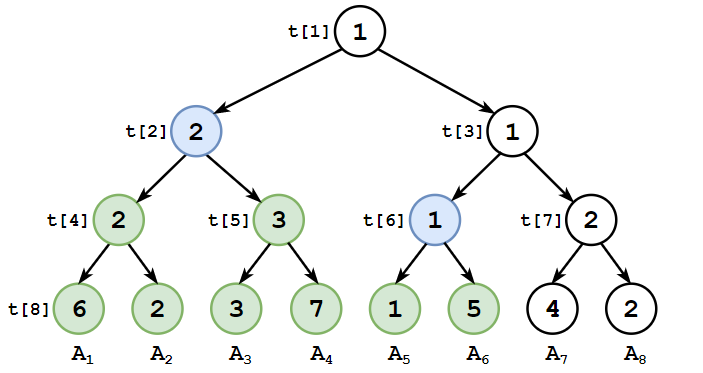
从根节点开始，自顶向下搜索出范围在 $[l,$$r]$ 之内的节点，这些节点的最小值即为答案。

$get(u,$$l,$$r)$：从节点 $u$ 开始，向下搜索 $A[l\cdots r]$ 的最小值。

1. 若 $u$ 的范围在 $[l,$$r]$ 之内，直接返回 $t[u]$；
2. 若 $u$ 的范围与 $[l,$$r]$ 不重叠，返回 $+$$\mathrm{\infty }$^[1]；
3. 否则递归搜索 $u$ 的两个子节点。

时间复杂度为 $O(\log n)$。

执行 $get(1,$$l,$$r)$ 以进行区间查询。

int get(int u, int l, int r) {
    if (l <= l(u) && r(u) <= r) return t(u);             // 1. 被包含
    if (l(u) > r || r(u) < l) return 0x3f3f3f;           // 2. 不重叠
    return min(get(2 * u, l, r), get(2 * u + 1, l, r)); // 3. 递归搜索
}

区间修改 + 延迟标记

如果一次性将 $A[3\cdots 8]$ 每个数加上 $v$，需要更新大量节点，时间复杂度接近 $O(n\log n)$。这不是我们希望看到的。

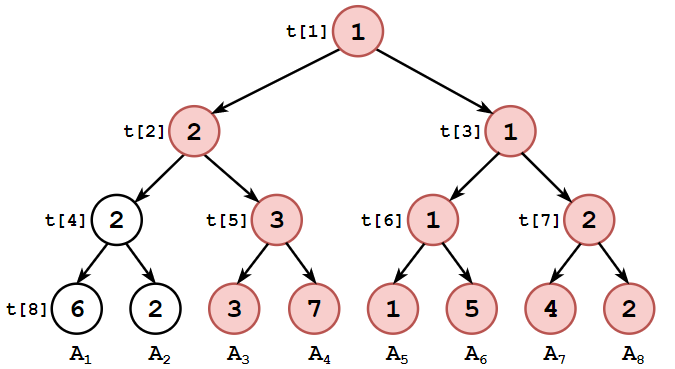
事实上，大部分节点用不着马上更新——直到它们再次被访问。于是我们可以先给部分节点打标记。

在本例中，$t[3]$ 和 $t[5]$ 被打上了标记，这代表它们的所有子节点都还没加上 $v$。

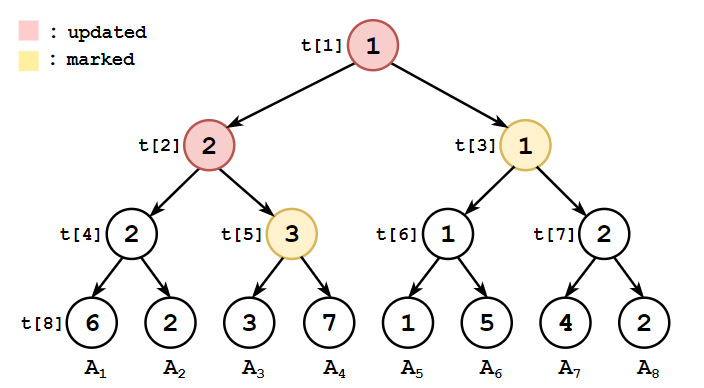
当访问 $A[5\cdots 6]$ 时，再更新 $t[3]$ 的左子树。$t[3]$ 的标记被下传到了它的右节点 $t[7]$。

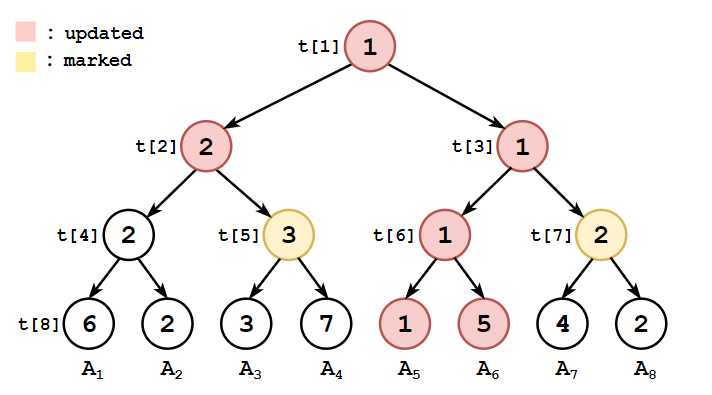
代码与 区间查询 类似。时间复杂度为 $O(\log n)$。

int mark[];

// 更新 u 的子节点，并下传标记
void spread(int u) {
    if (mark[u]) {
        t(2 * u) += mark[u];
        t(2 * u + 1) += mark[u];
        mark[2 * u] += mark[u];
        mark[2 * u + 1] += mark[u];
        mark[u] = 0;
    }
}

// 将 A[l] ... A[r] 加上 v
void add(int u, int l, int r, int v) {
    if (l <= l(u) && r(u) <= r) { // 完全覆盖
        t(u) += v, mark[u] += v; return; // 标记
    }
    else if (l(u) > r || r(u) < l) return;
    spread(u); // 下传标记
    int m = (l + r) / 2;
    add(2 * u, l, r, v);
    add(2 * u + 1, l, r, v);
    t(u) = min(t(2 * u), t(2 * u + 1));
}

同时，单点修改 和 区间查询 需要添加下传标记的操作。

void set(int u, int id, int v) {
    if (l(u) == r(u)) {
        a[id] = t(u) = v; return;
    }
    spread(u); // 下传标记
    int m = (l(u) + r(u)) / 2;
    if (id <= m) set(2 * u, id, v);
    else set(2 * u + 1, id, v);
    t(u) = min(t(2 * u), t(2 * u + 1));
}

int get(int u, int l, int r) {
    if (l <= l(u) && r(u) <= r) return t(u);
    else if (l(u) > r || r(u) < l) return 0x3f3f3f;
    spread(u); // 下传标记
    int m = (l + r) / 2;
    return min(get(2 * u, l, m), get(2 * u + 1, m + 1, r));
}

模板

struct Node {
    int val, l, r;
    #define t(u) t[u].val
    #define l(u) t[u].l
    #define r(u) t[u].r
} t[];

int mark[];

void build(int u, int l, int r) {
    l(u) = l, r(u) = r;
    if (l == r) {
        t(u) = a[l]; return;
    }
    int m = (l + r) / 2;
    build(2 * u, l, m);
    build(2 * u + 1, m + 1, r);
    t(u) = min(t(2 * u), t(2 * u + 1));
}

void spread(int u) {
    if (mark[u]) {
        t(2 * u) += mark[u];
        t(2 * u + 1) += mark[u];
        mark[2 * u] += mark[u];
        mark[2 * u + 1] += mark[u];
        mark[u] = 0;
    }
}

void set(int u, int id, int v) {
    if (l(u) == r(u)) {
        a[id] = t(u) = v; return;
    }
    spread(u);
    int m = (l(u) + r(u)) / 2;
    if (id <= m) set(2 * u, id, v);
    else set (2 * u + 1, id, v);
    t(u) = min(t(2 * u), t(2 * u + 1));
}

int get(int u, int l, int r) {
    if (l <= l(u) && r(u) <= r) return t(u);
    else if (l(u) > r || r(u) < l) return 0x3f3f3f;
    spread(u);
    int m = (l + r) / 2;
    return min(get(2 * u, l, m), get(2 * u + 1, m + 1, r));
}

void add(int u, int l, int r, int v) {
    if (l <= l(u) && r(u) <= r) {
        t(u) += v, mark[u] += v; return;
    }
    else if (l(u) > r || r(u) < l) return;
    spread(u);
    int m = (l + r) / 2;
    add(2 * u, l, r, v);
    add(2 * u + 1, l, r, v);
    t(u) = min(t(2 * u), t(2 * u + 1));
}

区间和线段树

线段树还可以查询区间和。

令每个节点代表一段区间的元素和，递推方程应为 $t[u]=$$t[2u]+$$t[2u+$$1]$。

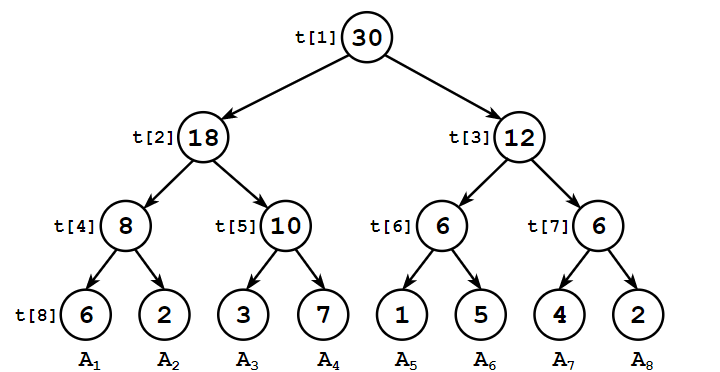
若 $t[u]$ 表示区间 $[l,$$r]$，而 $A[l]\cdots A[r]$ 都要加上 $v$，则 $t[u]$ 需要加上 $(r-$$l+$$1)\cdot v$。因此标记下传函数也需要调整。

void spread(int u) {
    if (mark[u]) {
        t(2 * u) += mark[u] * (l(2 * u) - r(2 * u) + 1);
        t(2 * u + 1) += mark[u] * (l(2 * u + 1) - r(2 * u + 1) + 1);
        mark[2 * u] += mark[u];
        mark[2 * u + 1] += mark[u];
        mark[u] = 0;
    }
}

---

1. $min\{+\mathrm{\infty },a\}=$$a$，因此返回 $\infty$ 相当于不参与最小值的比较。 ↩︎