Appearance
斐波那契数列
斐波那契数列是形如
分析
cpp
f[1] = f[2] = 1;
for (int i = 3; i <= n; i ++)
f[i] = f[i - 1] + f[i - 2];汉诺塔问题
汉诺塔由

现在,按以下规则将
- 一次只能动一个盘子;
- 盘子只能放在杆上;
- 大盘子不能叠在小盘子上。
求移动盘子的最少次数。
分析
将
- 将
杆的 个盘子移至 杆(共 次); - 将
杆的最后一个盘子移至 杆(共 次); - 将
杆的 个盘子移至 杆(共 次)。
cpp
f[1] = 1;
for (int i = 2; i <= n; i ++)
f[i] = 2 * f[i - 1] + 1;骨牌问题
用若干

求任意
分析
- 若第一个骨牌竖放在左边,则剩余
个空方格,铺法数为 ; - 若第一个骨牌横放在左上角,为了不留空,第二个骨牌必须横放在其正下方。剩余
个空方格,铺法数为 。
状态转移方程和 斐波那契数列 一致。
平面分割问题
平面上有
分析
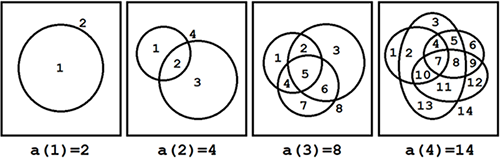
由上图可得:
即
正确性证明:
新增一条曲线时,每与一条已有曲线相交一次,就增加一个区域。而新增的第
cpp
a[1] = 2;
for (int i = 2; i <= n; i ++)
a[i] = a[i - 1] + 2 * (n - 1);最长上升子序列 (LIS)
求序列
例:
分析
枚举
- 若
,则 可以接在 后面,形成的上升子序列长度为 ; - 若
, 对 没有贡献,直接跳过。
问题的解是
cpp
for (int i = 1; i <= n; i ++) {
f[i] = 1;
for (int j = 1; j < i; j ++)
if (a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}单调栈优化
扫描每一个数,有策略地将其加入单调栈,使得栈的内容始终是当前的最长上升子序列。
举例来说,假设当前单调栈内有
当扫描到
- 若
大于栈尾,则直接将其入栈; - 否则在栈中二分查找第一个
的数,将其替换为 。
最终栈的长度即为 LIS 的长度。时间复杂度为
cpp
vector<int> s;
s.push_back(a[1]);
for (int i = 2; i <= n; i ++) {
if (a[i] > s.back())
s.push_back(a[i]);
else
*lower_bound(s.begin(), s.end(), a[i]) = a[i];
}最长公共子序列 (LCS)
求序列
例:freeze, refeze, reeze(长度
分析
- 枚举
: - 枚举
: - 首先继承最优子状态:
; - 若
,则 可以接在 之后,形成的公共序列长度为 。
- 首先继承最优子状态:
- 枚举
问题的解是
cpp
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= m; j ++) {
f[i][j] = max(f[i - 1][j], f[i][j - 1]);
if (a[i] == b[j])
f[i][j] = max(f[i][j], f[i - 1][j - 1] + 1);
}
}数字金字塔
三角矩阵
此例中,最优路径为
分析
逆推法:要走到
注意:当
问题的解是
cpp
memset(f, 0x80, sizeof f);
f[1][1] = 1;
for (int i = 2; i <= n; i ++) {
for (int j = 1; j <= i; j ++) {
cin >> f[i][j];
f[i][j] += max(f[i - 1][j - 1], f[i - 1][j]);
}
}
ans = 0;
for (int i = 1; i <= n; i ++)
ans = max(ans, f[n][i]);数字矩阵
有
此例中,最优路径为
分析
逆推法:由于只能向左走或向下走,要走到
注意:当
cpp
memset(f, 0x80, sizeof f);
for (int i = 1; i <= n; i ++) {
for (int j = 1; j <= m; j ++) {
cin >> f[i][j];
if (!(i == 1 && j == 1))
f[i][j] += max(f[i-1][j], f[i][j - 1]);
}
}前缀和
前缀和是一种重要的预处理技巧,能大幅降低查询数列的 连续元素之和 的时间复杂度。
预处理
数列
时间复杂度:
cpp
for (int i = 1; i <= n; i ++)
f[i] = f[i - 1] + a[i];查询
单次查询的时间复杂度:
cpp
// sum of a[i ... j]
int g(int i, int j) {
return f[j] - f[i - 1];
}二维前缀和
预处理
矩阵
时间复杂度:
cpp
f[0][0] = 0;
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];查询
单次查询的时间复杂度:
cpp
int g(int x1, int y1, int x2, int y2) {
return f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1];
}差分
差分是 前缀和 的逆运算,能大幅降低区间修改的时间复杂度。
预处理
数列
令
时间复杂度:
cpp
for (int i = 1; i <= n; i ++)
f[i] = a[i] - a[i - 1];区间修改
当给
因此可以每次只修改
单次修改的时间复杂度:
cpp
void add(int l, int r, int x) { // add x to A[l ... r]
f[l] += x, f[r + 1] -= x;
}
void restore() {
for(int i = 1; i <= n; i ++)
a[i] = a[i - 1] + f[i];
}