快速傅里叶变换能在 $O(n\log n)$ 的时间复杂度下计算两个 $n$ 次多项式的乘法。

多项式的表示法

系数表示法

对于 $n-$$1$ 次多项式

$$A(x)=a_0+a_{1}x+a_2{x}^2+\cdots +a_{n-1}{x}^{n-1}$$

系数表示法用 $n$ 个系数表示它。

$$\{a_0,a_1,\cdots ,a_{n-1}\}$$

点值表示法

两点确定 $kx+$$b$，三点确定 $a{x}^2+$$bx+$$c$，以此类推。至少 $n$ 点才能确定 $n-$$1$ 次多项式。

点值表示法用至少 $n$ 个不同的点表示 $n-$$1$ 次多项式。

$$\{(x_0,y_0),(x_1,y_1),\cdots ,(x_{n-1},y_{n-1})\}$$

多项式乘法

离散傅里叶变换（Discrete Fourier Transform，DFT）是将多项式从 系数表示法 转换为 点值表示法 的算法，IDFT 是 DFT 的逆过程。

运用 DFT 和 IDFT 计算多项式乘法 $A(x)\cdot B(x)=$$C(x)$ 的主要步骤：

1. 对 $A(x)$ 和 $B(x)$ 使用 DFT，得到两个点集：$$\begin{gathered} \{(x_i,A(x_i))\mid 0\le i<N\} \\ \{(x_i,B(x_i))\mid 0\le i<N\} \end{gathered}$$
2. 计算出 $C(x)$ 的点值表示法：$$\{(x_i,A(x_i)\cdot B(x_i))\mid 0\le i<N\}$$
3. 使用 IDFT 将其转化为系数表示法。

其中 $N\ge C(x)\text{的次数}+$$1=$$A(x)\text{的次数}+$$B(x)\text{的次数}+$$1$，否则第二步得到的点太少，不足以确定最终的答案。

一般的 DFT 和 IDFT 时间复杂度高达 $O(n^2)$，而快速傅里叶变换（Fast Fourier Transform，FFT）可以把这个过程优化到 $O(n\log n)$。

让我们从一个例子入手，先熟悉一下 $O(n^2)$ 的普通算法是什么样的。

普通的算法

现在计算 $A(x)=$$x^2+$$x+$$1$ 和 $B(x)=$$x^2-$$3$ 的乘积 $C(x)$。

这个乘法的结果肯定是一个 $4$ 次的多项式，这意味着我们至少要取 $5$ 个点，那么就随便取 $x=$$1,$$2,$$3,$$4,$$5$ 好了。

第一步：计算 $A(x)$ 和 $B(x)$ 的点值表示法：

$$\begin{array}{rl}& A(x)⟶\{(1,3),(2,7),(3,13),(4,21),(5,31)\}\\ & B(x)⟶\{(1,-2),(2,1),(3,6),(4,13),(5,22)\}\end{array}$$

第二步：计算 $C(x)=$$A(x)\cdot B(x)$ 的点值表示法：

$$C(x)⟶\{(1,-6),(2,7),(3,78),(4,273),(5,682)\}$$

第三步：转化为系数表示法。这一步的方法有很多，可以使用拉格朗日插值法等。总之最后算出来的结果是

$$C(x)=x^4\hspace{0.17em}+\hspace{0.17em}{x}^3\hspace{0.17em}-\hspace{0.17em}2x^2\hspace{0.17em}-\hspace{0.17em}3x\hspace{0.17em}-\hspace{0.17em}3$$

当 $C(x)$ 是 $n-$$1$ 次多项式时，需要取 $n$ 个不同的 $x$。其中每次计算 $A(x)\cdot B(x)$ 的时间复杂度为 $O(n)$，并且这个过程要重复 $n$ 次，那么总的时间复杂度为 $O(n^2)$。

---

上述流程存在一个比较现实的问题：在实际的应用场景中，多项式的次数往往很大。如果我们随意地取 $x$ 的值，计算出的 $A(x)$ 可能会超出基本变量类型的范围，那么这个算法很有可能在第一步就会搁浅。

所以 $x$ 的取值其实很有门道。它既不能让 $A(x)$ 太大，让计算机存不下；也不能让 $\parallel A(x)\parallel$ 太小，导致计算过程中发生精度的损失。这么看来，似乎只有 $0$，$1$ 和 $-$$1$ 这三个数比较合适。

但是只有这三个数是远远不够的。去哪里找其它的数呢？

这样的数，数学家们在复数域中找到了无穷多个。

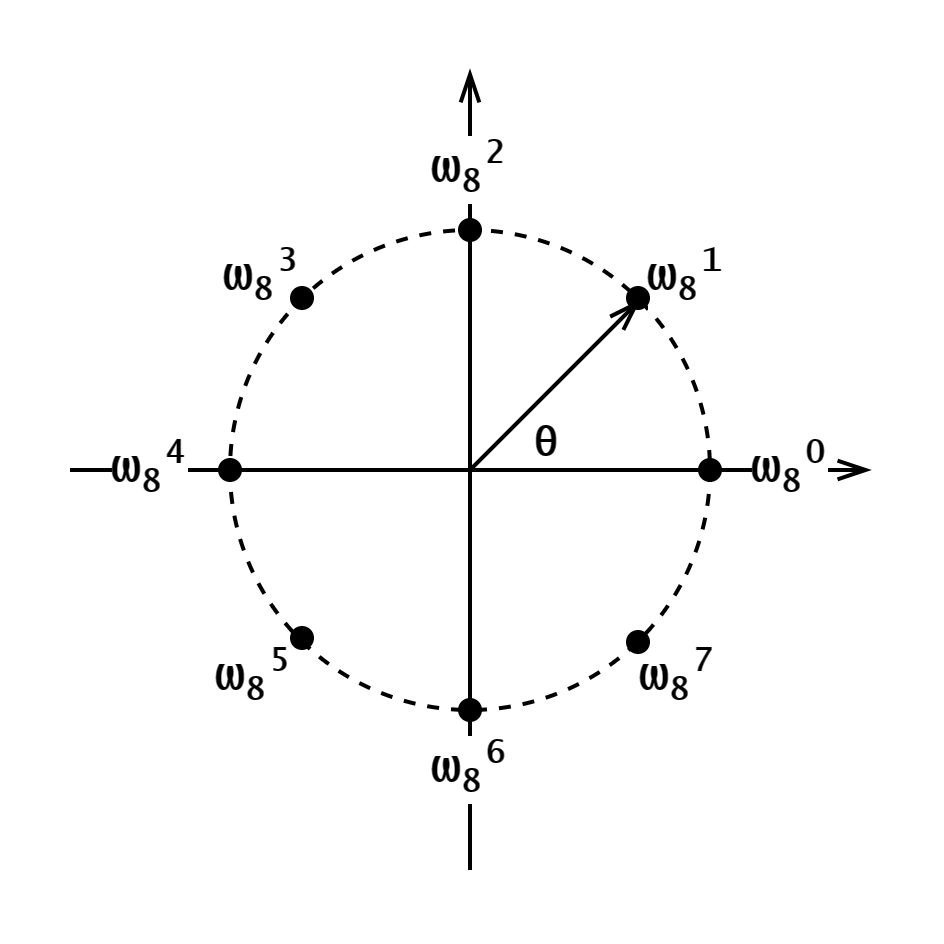
单位复根

复习

形如 $a+$$bi$（$a$、$b$ 均为实数）的数为复数。其中

• $a$ 被称为实部；
• $b$ 被称为虚部；
• $i$ 是虚数单位，$i^2=$$-$$1$；
• $\sqrt{a^2+b^2}$ 是这个复数的模。

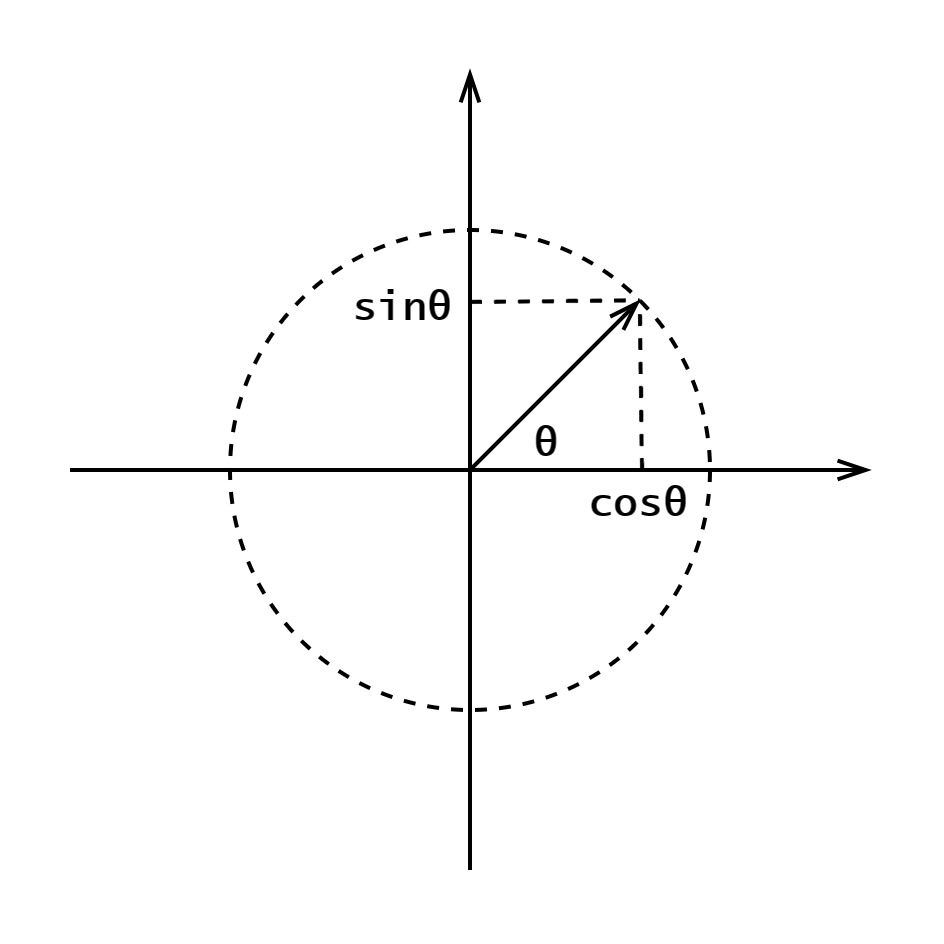
在复平面上，$a+$$bi$ 对应的坐标为 $(a,$$b)$。其中

• $a$ 表示的是复平面内的横坐标；
• $b$ 表示的是复平面内的纵坐标；
• 表示实数 $a$ 的点都在 $x$ 轴上，所以 $x$ 轴又称为「实轴」；
• 表示纯虚数 $bi$ 的点都在 $y$ 轴上，所以 $y$ 轴又称为「虚轴」。

如图 1，在复平面上画一个半径为 $1$ 的单位圆。圆上的每一点 $(\cos \theta ,$$\sin \theta )$ 都可以表示复数 $\cos \theta +$$i\sin \theta$，其中 $\theta$ 是幅角，即它和原点的连线与实轴正半轴的夹角。

如果把圆周角 $N$ 等分，也就是令 $\theta =$$\frac{2\pi }{N}$，那么这个复数就被称作 单位复根，记作 ${\omega }_N$。

$${\omega }_N=\cos \frac{2\pi }{N}+i\sin \frac{2\pi }{N}$$

中学课本告诉了我们复数乘法的规律：幅角相加模相乘。我们知道 ${\omega }_N$ 的模为 $1$，那么 ${\omega }_N^k$ 的模也就还是 $1$，且其幅角从原来的 $\frac{2\pi }{N}$ 变成了 $\frac{2k\pi }{N}$。

根据上述规律，不难发现，${\omega }_N^0,$${\omega }_N^1,$${\omega }_N^2,$$\cdots ,$${\omega }_N^{N-1}$ 在单位圆上的分布是均匀的。图 2 展示了 $N=$$8$ 时的情况。

图 1	图 2

单位复根还具有如下优异的性质：

1. 周期性：${\omega }_N^N=$$1$；
2. 消去性：${\omega }_{2N}^{2k}=$${\omega }_N^k$；
3. 对称性：${\omega }_N^{k+\frac{N}{2}}=$$-$${\omega }_N^k$。

证明并不困难。一方面可以用上文中 ${\omega }_N^k$ 的图像性质去推理；另一方面，直接套用欧拉公式

$$e^{i\theta }=\cos \theta +i\sin \theta \Rightarrow {\omega }_N=e^{\frac{2\pi }{N}i}$$

也能能轻易得证。

---

单位复根 恰好可以完美地解决 DFT 中取点的问题。代入 $x=$${\omega }_N^k$ 既不会使 $y=$$A(x)$ 大到溢出，也不会使其小到失真，唯一别扭的地方就是 $x$ 和 $y$ 都是复数值。不过大部分编程语言都有支持复数运算的库，所以这不是大问题。因此当我们需要在 DFT 中取 $N$ 个点时，不妨取

$$x={\omega }_N^0,{\omega }_N^1,{\omega }_N^2,\cdots ,{\omega }_N^{N-1}$$

但是，单位复根仅解决了精度问题。目前为止，时间复杂度仍然是 $O(n^2)$。真正使其成为「快速」傅里叶变换的，是接下来的「多项式分治」。

多项式分治

对一个 $n$ 项的多项式

$$A(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+\cdots +a_{n-2}{x}^{n-2}+a_{n-1}{x}^{n-1}$$

进行如下变换（假定 $n=$$2^k,$$k\in \mathbb{Z}$）：

1. 将偶数项留在前面，将奇数项移到后面：

$$A(x)=a_0+a_2{x}^2+\cdots +a_{n-2}{x}^{n-2}+a_{1}x+a_3{x}^3+\cdots +a_{n-1}{x}^{n-1}$$

2. 对后一半提取公因式 $x$：

$$A(x)=a_0+a_2{x}^2+\cdots +a_{n-2}{x}^{n-2}+x\cdot (a_1+a_3{x}^2+\cdots +a_{n-1}{x}^{n-2})$$

设

$$A_{\mathrm{even}}(x)=a_0+a_{2}x+\cdots +a_{n-2}{x}^{\frac{n}{2}-1}$$$$A_{\mathrm{odd}}(x)=a_1+a_{3}x+\cdots +a_{n-1}{x}^{\frac{n}{2}-1}$$

则

$$A(x)=A_{\mathrm{even}}\left(x^2\right)+x\cdot A_{\mathrm{odd}}\left(x^2\right)$$

注意这里我们将 $x^2$ 作为 $A_{\mathrm{even}}$ 和 $A_{\mathrm{odd}}$ 的变量。

将 $x=$${\omega }_n^k$ 代入得：

$$\begin{array}{rl}A\left({\omega }_n^k\right)& =A_{\mathrm{even}}\left({\omega }_n^{2k}\right)+{\omega }_n^k\cdot A_{\mathrm{odd}}\left({\omega }_n^{2k}\right)\\ & =A_{\mathrm{even}}\left({\omega }_{n/2}^k\right)+{\omega }_n^k\cdot A_{\mathrm{odd}}\left({\omega }_{n/2}^k\right)\end{array}$$

将 $x=$${\omega }_n^{k+n/2}=$$-$${\omega }_n^k$ 代入得：

$$\begin{array}{rl}A\left({\omega }_n^{k+n/2}\right)& =A(-{\omega }_n^k)\\ & =A_{\mathrm{even}}\left({\omega }_{n/2}^k\right)-{\omega }_n^k\cdot A_{\mathrm{odd}}\left({\omega }_{n/2}^k\right)\end{array}$$

我们发现，$A_{\mathrm{even}}\left({\omega }_{n/2}^k\right)$ 和 $A_{\mathrm{odd}}\left({\omega }_{n/2}^k\right)$ 各自又都是 $n/$$2$ 项多项式，它们也可以用同样的方法再往下拆分成更短的多项式之和。所以我们采用递归的方式去实现这个计算过程。

对每个 $A\left({\omega }_n^k\right)$ 单独递归的效率太低。这里采用的递归策略是：先计算出

$$\{A_{\mathrm{even}}\left({\omega }_{n/2}^0\right),A_{\mathrm{even}}\left({\omega }_{n/2}^1\right),\cdots ,A_{\mathrm{even}}\left({\omega }_{n/2}^{n/2-1}\right)\}$$$$\{A_{\mathrm{odd}}\left({\omega }_{n/2}^0\right),A_{\mathrm{odd}}\left({\omega }_{n/2}^1\right),\cdots ,A_{\mathrm{odd}}\left({\omega }_{n/2}^{n/2-1}\right)\}$$

再根据之前推出的公式

$$\{\begin{array}{lllll}A\left({\omega }_n^k\right)& =& A_{\mathrm{even}}\left({\omega }_{n/2}^k\right)& +& {\omega }_n^k\cdot A_{\mathrm{odd}}\left({\omega }_{n/2}^k\right)\\ \\ A\left({\omega }_n^{k+n/2}\right)& =& A_{\mathrm{even}}\left({\omega }_{n/2}^k\right)& -& {\omega }_n^k\cdot A_{\mathrm{odd}}\left({\omega }_{n/2}^k\right)\end{array}k=0,1,\cdots ,\frac{n}{2}-1$$

得出

$$\{A\left({\omega }_n^0\right),A\left({\omega }_n^1\right),\cdots ,A\left({\omega }_n^{n-1}\right)\}$$

进而得出我们所需要的 $n$ 个点值。

---

设 $a=$$\{a_0,a_1,\cdots ,a_{n-1}\}$ 是存放 $A(x)$ 系数的数组，函数 $\mathrm{DFT}(a)$ 的功能是算出并返回

$$\{A\left({\omega }_n^0\right),A\left({\omega }_n^1\right),\cdots ,A\left({\omega }_n^{n-1}\right)\}$$

以下是 $\mathrm{DFT}(a)$ 的伪代码：

$$\begin{array}{rl}& \mathrm{DFT}(a):\\ & n:=a.\mathrm{size}()\\ & \mathrm{If}n=1:\\ & \mathrm{return}a\\ & y^{\mathrm{even}}:=\mathrm{DFT}(\{a_0,a_2,\cdots ,a_{n-2}\})\\ & y^{\mathrm{odd}}:=\mathrm{DFT}(\{a_1,a_3,\cdots ,a_{n-1}\})\\ & y:=\{\}\\ & \omega :=1\\ & {\omega }_n:=\cos \frac{2\pi }{n}+i\sin \frac{2\pi }{n}\\ & \mathrm{For}k=0\cdots \frac{n}{2}-1:\\ & y_k=y_k^{\mathrm{even}}+\omega \ast y_k^{\mathrm{odd}}\\ & y_{k+\frac{n}{2}}=y_k^{\mathrm{even}}-\omega \ast y_k^{\mathrm{odd}}\\ & \omega =\omega \ast {\omega }_n\\ & \mathrm{return}y\end{array}$$

可以画出 $\mathrm{DFT}$ 算法的递归图：

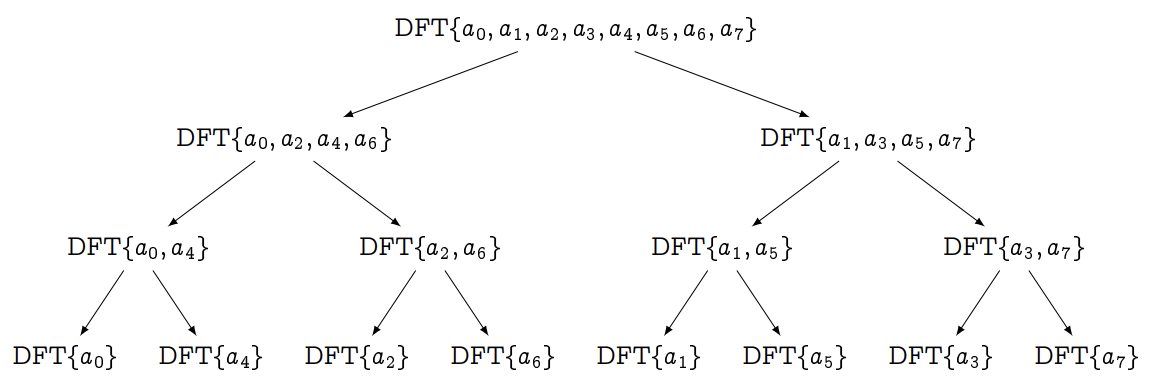
容易看出，以上分治算法每次都能递归地将规模为 $n$ 的问题拆分成两个规模为 $n/$$2$ 的问题，总时间复杂度为 $O(n\log n)$。

---

之所以在一开始假定 $n=$$2^k,$$k\in \mathbb{Z}$，就是为了确保每次对多项式进行拆分时都能恰好平均分为两半。如果多项式的项数 $n$ 不符合这个要求，那么我们可以往后面补 $0$ 项，直到达成这个要求。

例如对于 $A(x)=$$1+$$x+$$4x^2+$$5x^3+$$x^4+$$4x^5$ 一共只有 $6$ 项，还差 $2$ 项就能符合要求，所以往后面补两个 $0$ 项：

$$A(x)=1+x+4x^2+5x^3+x^4+4x^5+0x^6+0x^7$$

---

以上就是 FFT 加速算法的全部内容。不过我们只是用它加速了 DFT 的过程。多项式乘法的最后一步，也就是 IDFT，我们仍然没有提及。实际上 IDFT 也可以用同样的算法进行加速。

IDFT

前文所论述的 DFT 算法实际上是在解以下方程组：

$$\{\begin{array}{lllllllllll}{a}_0& +& a_1& +& a_2& +& \cdots & +& a_{n-1}& =& y_0\\ a_0& +& a_1\left({\omega }_n\right)& +& a_2{\left({\omega }_n\right)}^2& +& \cdots & +& a_{n-1}{\left({\omega }_n\right)}^{n-1}& =& y_1\\ a_0& +& a_1\left({\omega }_n^2\right)& +& a_2{\left({\omega }_n^2\right)}^2& +& \cdots & +& a_{n-1}{\left({\omega }_n^2\right)}^{n-1}& =& y_2\\ & & & & & & \cdots \\ a_0& +& a_1\left({\omega }_n^{n-1}\right)& +& a_2{\left({\omega }_n^{n-1}\right)}^2& +& \cdots & +& a_{n-1}{\left({\omega }_n^{n-1}\right)}^{n-1}& =& y_{n-1}\end{array}$$

令 $\mathbf{A}=$$\left(\begin{array}{c}{a}_0\\ a_1\\ a_2\\ ⋮\\ a_{n-1}\end{array}\right)$，$\mathbf{Y}=$$\left(\begin{array}{c}{y}_0\\ y_1\\ y_2\\ ⋮\\ y_{n-1}\end{array}\right)$，则上述方程组可以写成矩阵乘法的形式：

$$\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& {\omega }_n& {\left({\omega }_n\right)}^2& \cdots & {\left({\omega }_n\right)}^{n-1}\\ 1& {\omega }_n^2& {\left({\omega }_n^2\right)}^2& \cdots & {\left({\omega }_n^2\right)}^{n-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }_n^{n-1}& {\left({\omega }_n^{n-1}\right)}^2& \cdots & {\left({\omega }_n^{n-1}\right)}^{n-1}\end{array}\right)\cdot \mathbf{A}=\mathbf{Y}$$

DFT 的数学本质就是已知 $\mathbf{A}$，求解 $\mathbf{Y}$。而 IDFT 作为其逆过程，实际上就是已知 $\mathbf{Y}$，求解 $\mathbf{A}$。这正好对应了从点值表示法向系数表示法的转换。

为了实现 IDFT，我们可以很自然地对上式做出以下变换：

$$\mathbf{A}={\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& {\omega }_n& {\left({\omega }_n\right)}^2& \cdots & {\left({\omega }_n\right)}^{n-1}\\ 1& {\omega }_n^2& {\left({\omega }_n^2\right)}^2& \cdots & {\left({\omega }_n^2\right)}^{n-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }_n^{n-1}& {\left({\omega }_n^{n-1}\right)}^2& \cdots & {\left({\omega }_n^{n-1}\right)}^{n-1}\end{array}\right)}^{-1}\cdot \mathbf{Y}$$

那怎么求中间的这个逆矩阵呢？我们一眼就可以盯真出这是个特殊范德蒙矩阵的逆矩阵。

范德蒙矩阵求逆的特殊情况

在范德蒙矩阵中，当 $x_1=$$x_2=$$\cdots =$$x_n=$$x$ 时，有

$${\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& x& x^2& \cdots & x^{n-1}\\ 1& x^2& x^4& \cdots & x^{2(n-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x^{n-1}& x^{2(n-1)}& \cdots & x^{(n-1)(n-1)}\end{array}\right)}^{-1}=\frac{1}{n}\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& x^{n-1}& x^{2(n-1)}& \cdots & x^{(n-1)(n-1)}\\ 1& x^{(n-2)}& x^{2(n-2)}& \cdots & x^{(n-2)(n-1)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x& x^2& \cdots & x^{n-1}\end{array}\right)$$

再结合 单位复根 的性质就可以得出

$${\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& {\omega }_n& {\left({\omega }_n\right)}^2& \cdots & {\left({\omega }_n\right)}^{n-1}\\ 1& {\omega }_n^2& {\left({\omega }_n^2\right)}^2& \cdots & {\left({\omega }_n^2\right)}^{n-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }_n^{n-1}& {\left({\omega }_n^{n-1}\right)}^2& \cdots & {\left({\omega }_n^{n-1}\right)}^{n-1}\end{array}\right)}^{-1}=\frac{1}{n}\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& {\omega }_n^{-1}& {\left({\omega }_n^{-1}\right)}^2& \cdots & {\left({\omega }_n^{-1}\right)}^{n-1}\\ 1& {\omega }_n^{-2}& {\left({\omega }_n^{-2}\right)}^2& \cdots & {\left({\omega }_n^{-2}\right)}^{n-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& {\omega }_n^{-(n-1)}& {\left({\omega }_n^{-(n-1)}\right)}^2& \cdots & {\left({\omega }_n^{-(n-1)}\right)}^{n-1}\end{array}\right)$$

再将这个结果代入进去，并还原成方程组：

$$\{\begin{array}{lllllllllll}{y}_0& +& y_1& +& y_2& +& \cdots & +& y_{n-1}& =& n\cdot a_0\\ y_0& +& y_1\left({\omega }_n^{-1}\right)& +& y_2{\left({\omega }_n^{-1}\right)}^2& +& \cdots & +& y_{n-1}{\left({\omega }_n^{-1}\right)}^{n-1}& =& n\cdot a_1\\ y_0& +& y_1\left({\omega }_n^{-2}\right)& +& y_2{\left({\omega }_n^{-2}\right)}^2& +& \cdots & +& y_{n-1}{\left({\omega }_n^{-2}\right)}^{n-1}& =& n\cdot a_2\\ & & & & & & \cdots \\ y_0& +& y_1\left({\omega }_n^{-(n-1)}\right)& +& y_2{\left({\omega }_n^{-(n-1)}\right)}^2& +& \cdots & +& y_{-(n-1)}{\left({\omega }_n^{-(n-1)}\right)}^{n-1}& =& n\cdot a_{n-1}\end{array}$$

这个方程组和原先的方程组极为相似。这意味着我们只需调整 DFT 代码中某些参数的正负号，并且将最终的结果除以 $n$，就能得到 IDFT 的代码。

模板

#include <bits/stdc++.h>
using namespace std;

typedef complex<double> Comp;
const double PI = acos(-1);

vector<Comp> DFT(vector<Comp> a, bool invert) {
    int n = a.size();
    if (n == 1) return a;

    vector<Comp> a0(n / 2), a1(n / 2);
    for (int i = 0; 2 * i < n; i ++) {
        a0[i] = a[2*i];
        a1[i] = a[2*i + 1];
    }

    vector<Comp> y0 = DFT(a0, invert);
    vector<Comp> y1 = DFT(a1, invert);
    vector<Comp> y(n);

    double angle = 2 * PI / n * (invert ? -1 : 1);
    Comp w(1), wn(cos(angle), sin(angle));
    
    for (int i = 0; i < n / 2; i++) {
        y[i] = y0[i] + w * y1[i];
        y[i + n/2] = y0[i] - w * y1[i];
        if (invert) {
            y[i] /= 2;
            y[i + n/2] /= 2;
        }
        w *= wn;
    }
    
    return y;
}

vector<Comp> multiply(vector<Comp> A, vector<Comp> B) {
    int n = 1;
    while (n < A.size() + B.size()) 
        n *= 2;
    A.resize(n);
    B.resize(n);

    vector<Comp> yA = DFT(A, false);
    vector<Comp> yB = DFT(B, false);
    vector<Comp> yC(n);

    for (int i = 0; i < n; i ++)
        yC[i] = yA[i] * yB[i];

    vector<Comp> C = DFT(yC, true);

    for (int i = 0; i < n; i ++)
        C[i] = round(C[i].real());

    while (C.size() && ! C.back().real())
        C.pop_back();

    return C;
}

int main() {
    vector<Comp> A = {1, 2, 3}; // Represents the polynomial 1 + 2x + 3x^2
    vector<Comp> B = {4, 5};    // Represents the polynomial 4 + 5x
    
    vector<Comp> C = multiply(A, B);
    
    for (auto i : C)
        cout << i.real() << ' ';
    cout << endl;
    
    return 0;
}