Appearance
需要 极点极线方程 的相关知识。
定义
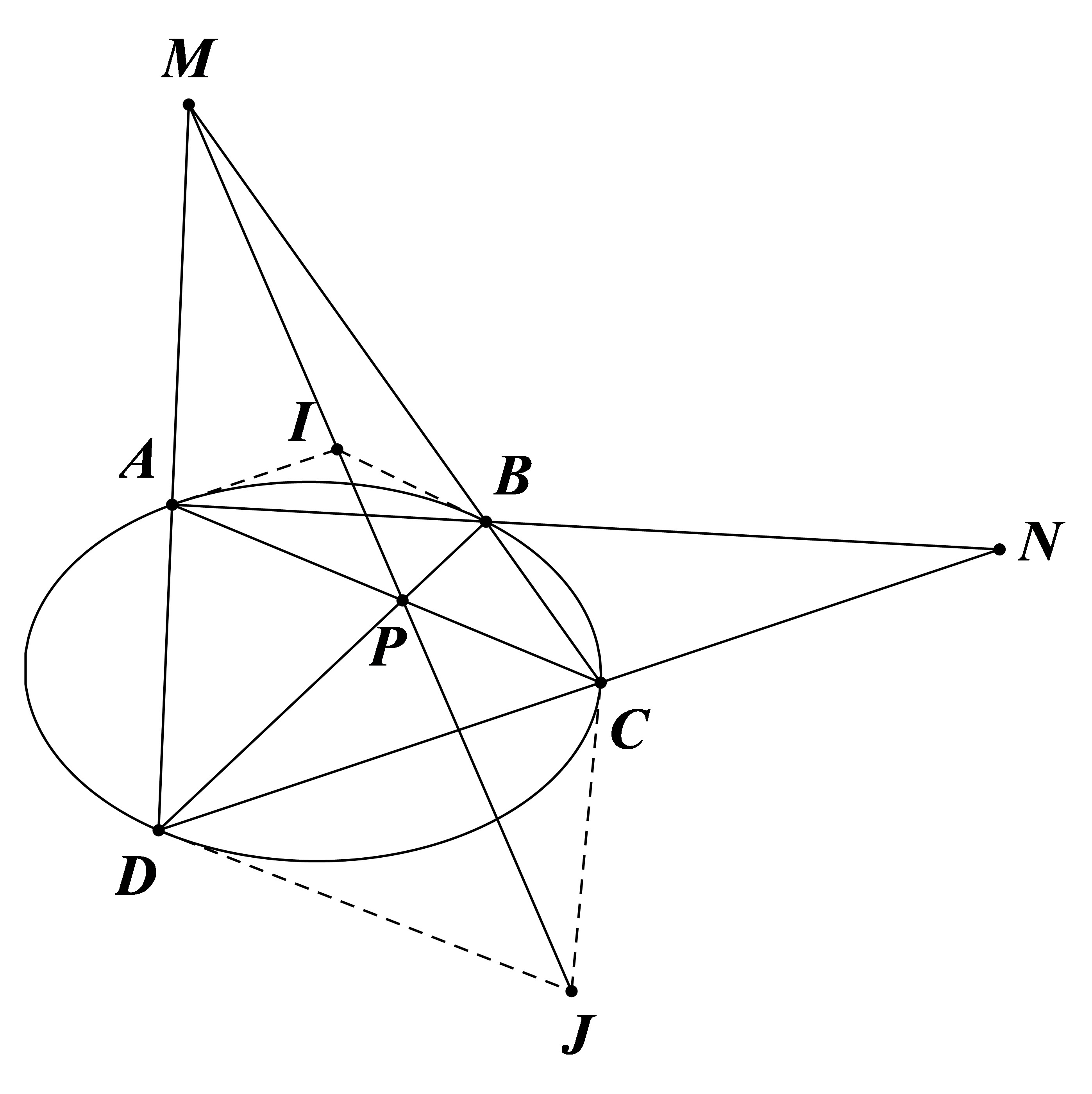
圆锥曲线任意内接四边形
是 的极线; 是 的极线; 是 的极线。
证明
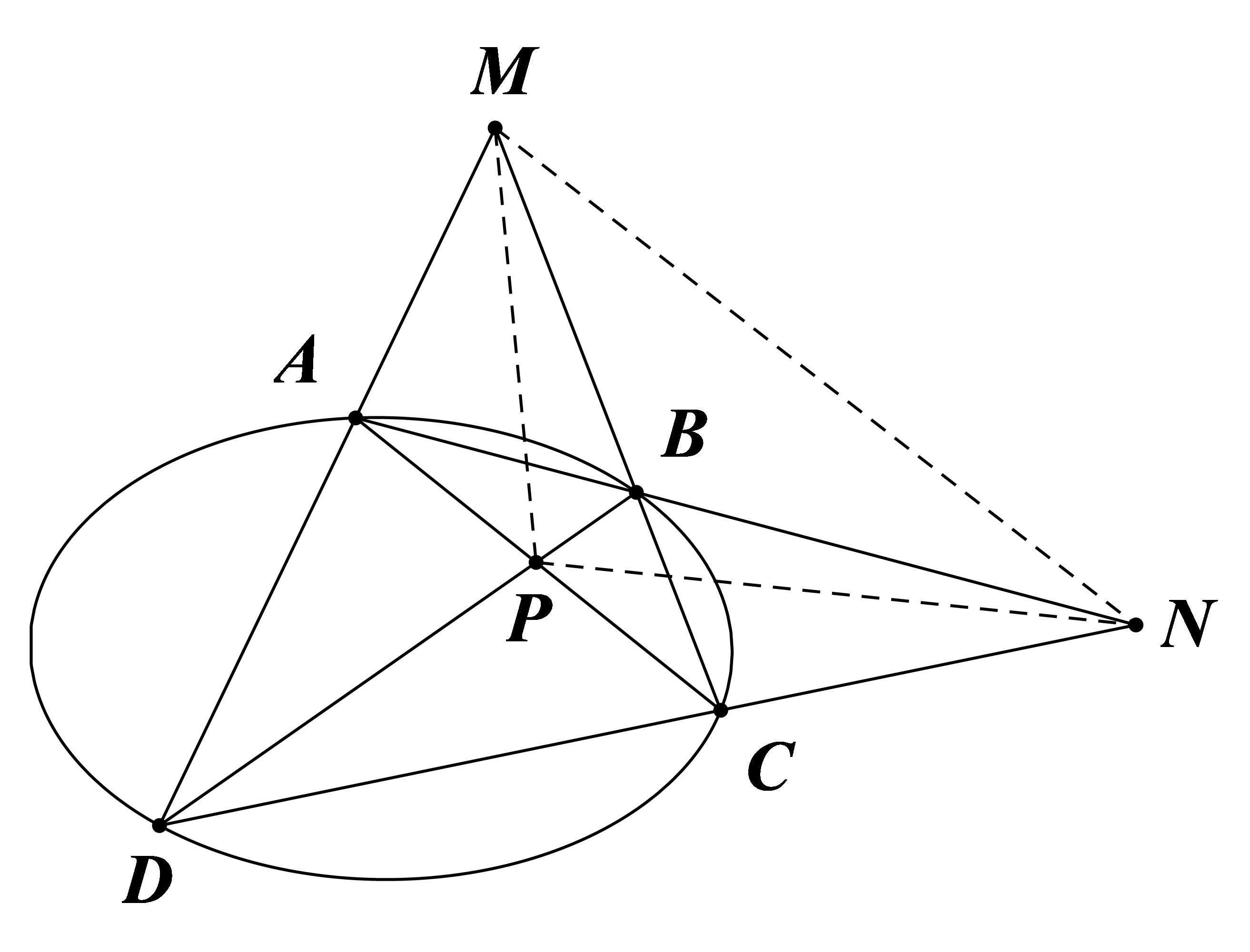
引理
Ceva 定理
证
代入即得
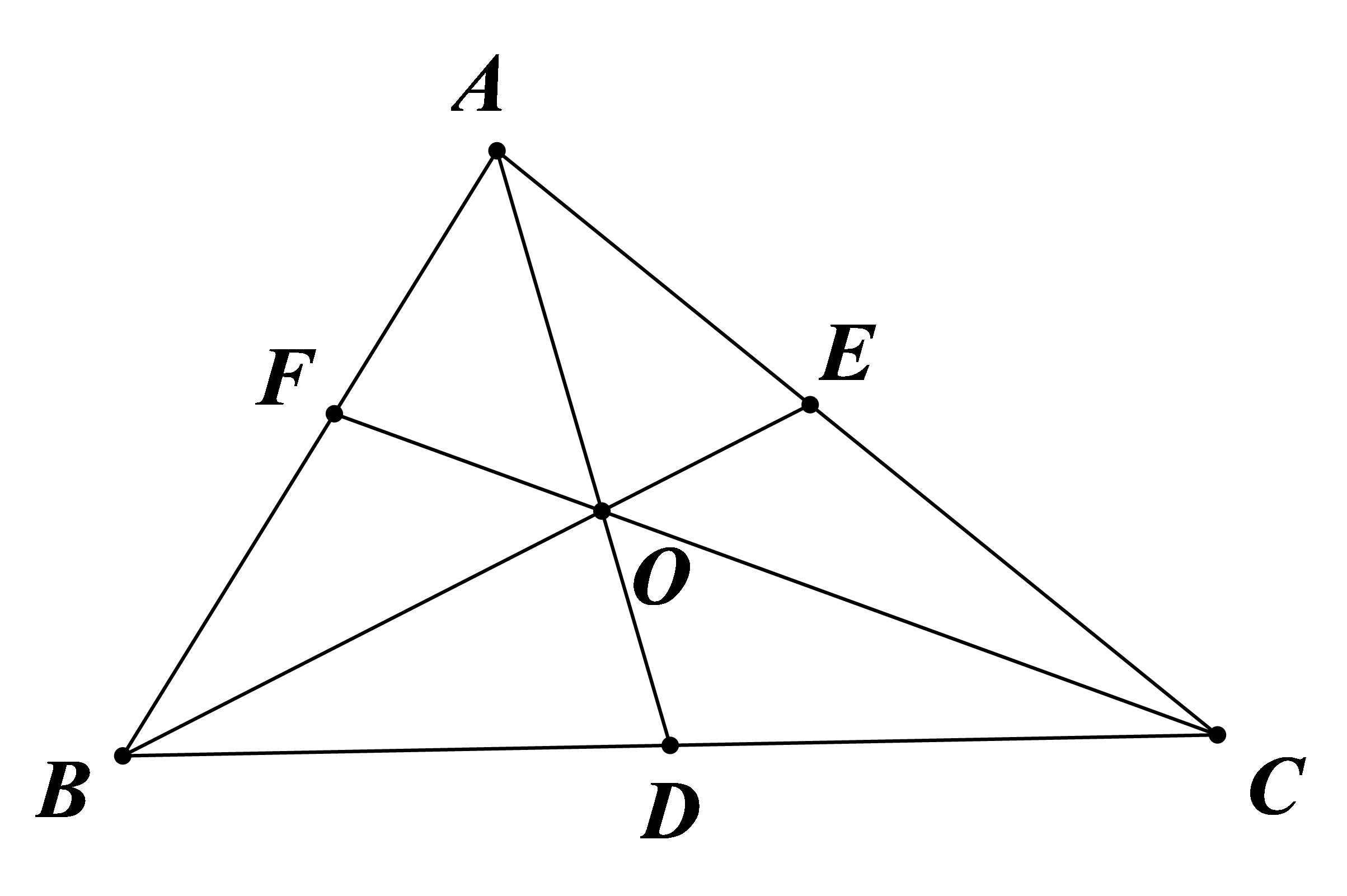
Ceva 定理还有角元形式
证明过程与边元形式大致相同。
证明过程都是充要的,故 Ceva 定理可逆用。
Pascal 定理
二次曲线任意内接六边形的所有对边交点共线。
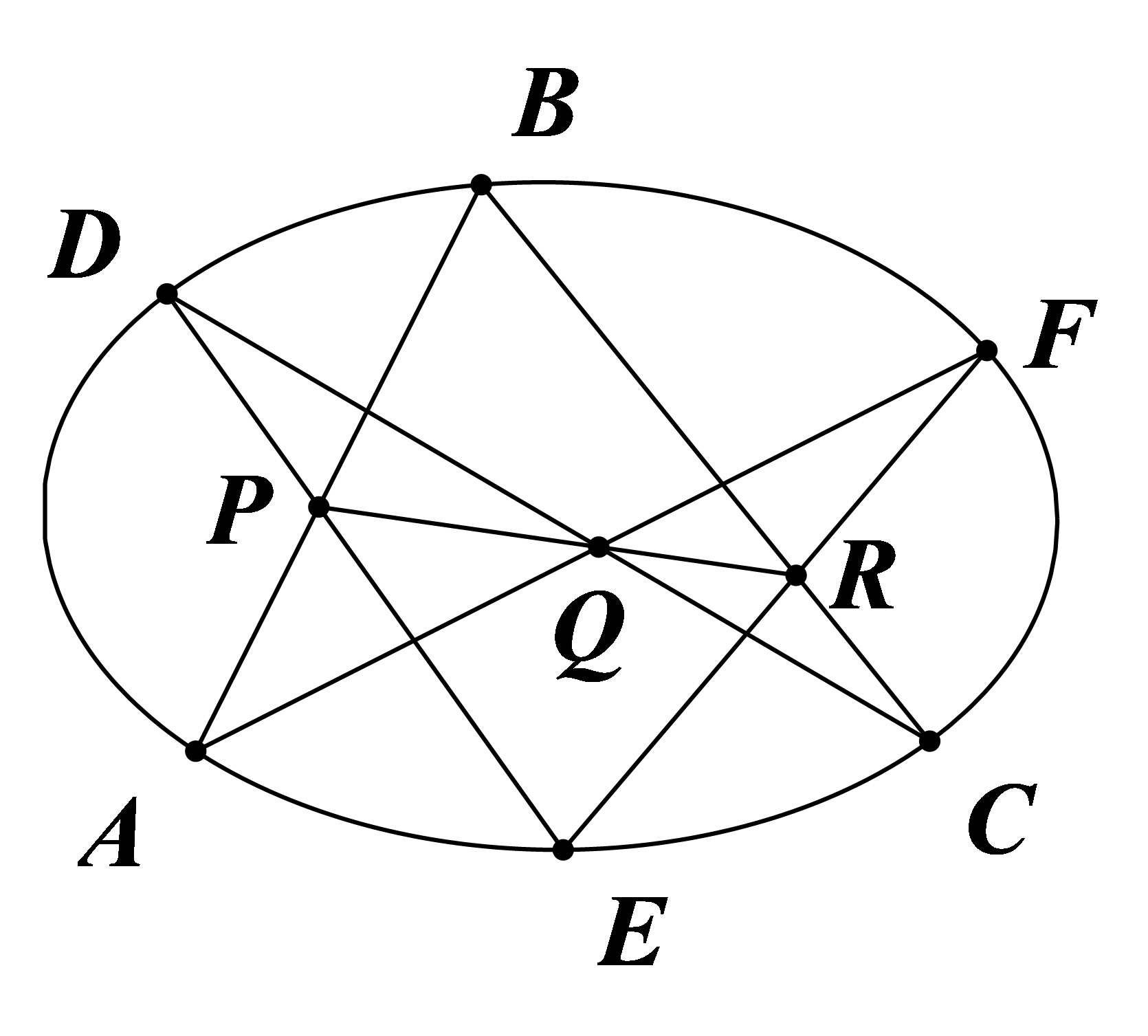
证明
移动 Pascal 定理 中六个顶点的位置。
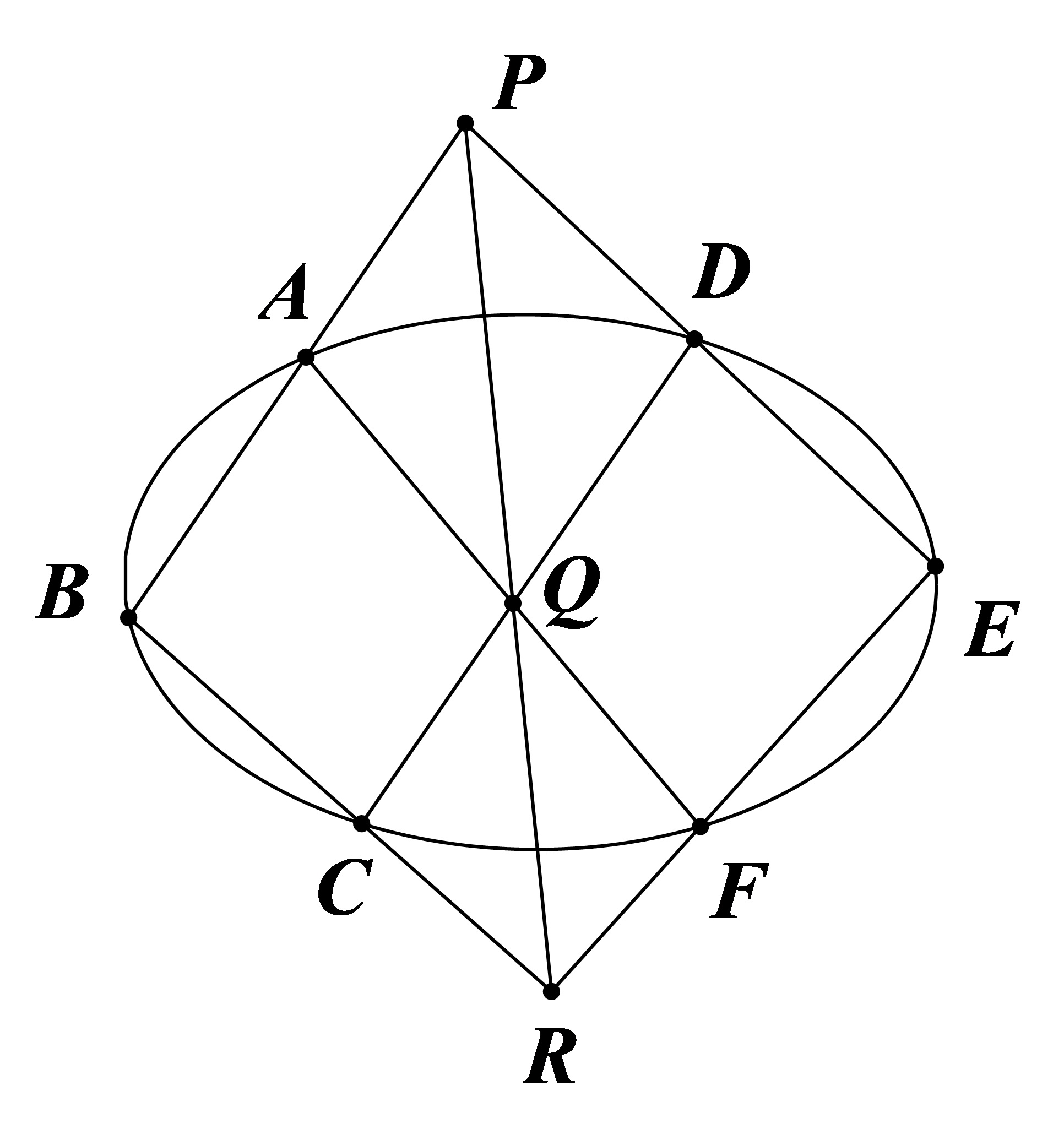
当
同理,再将
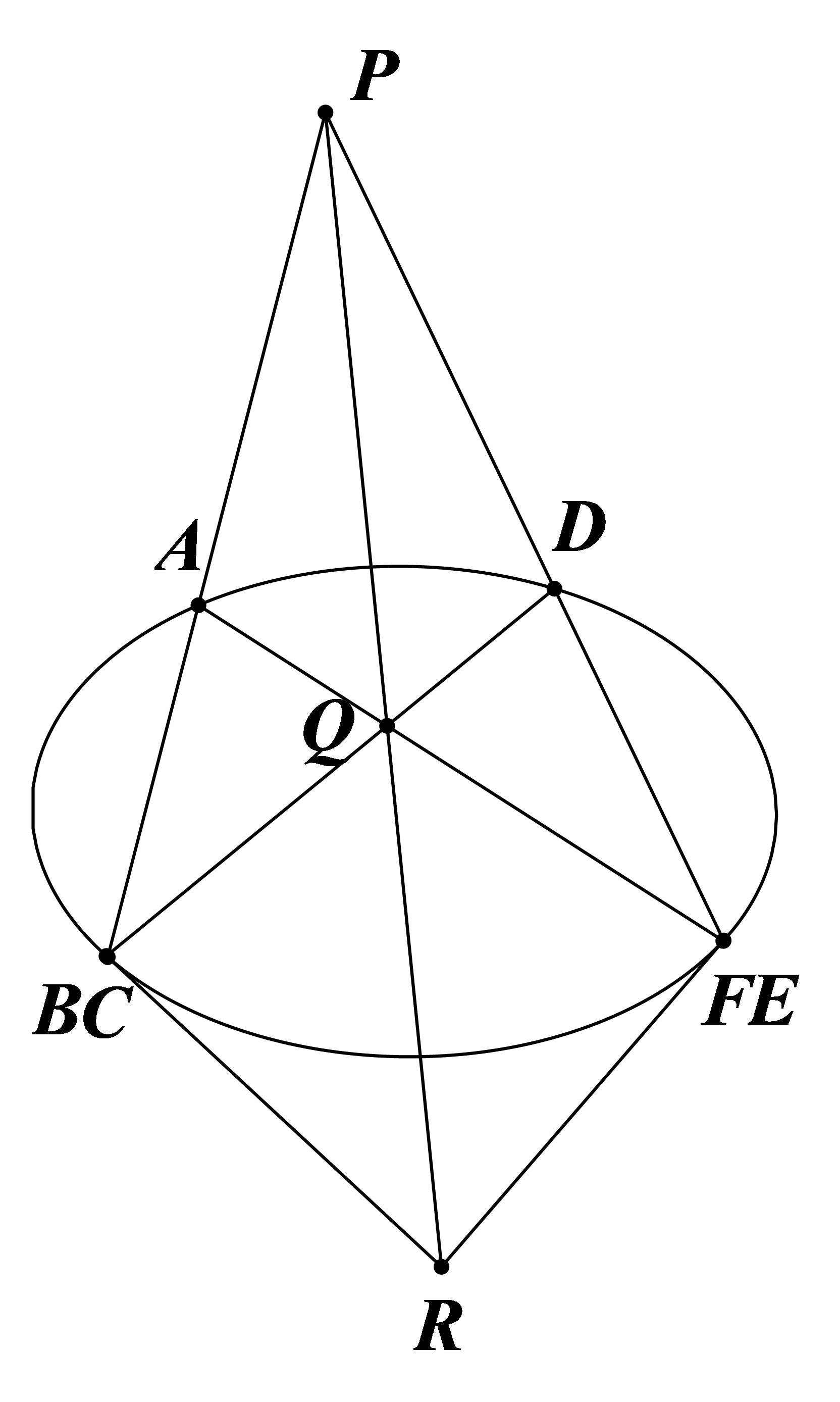
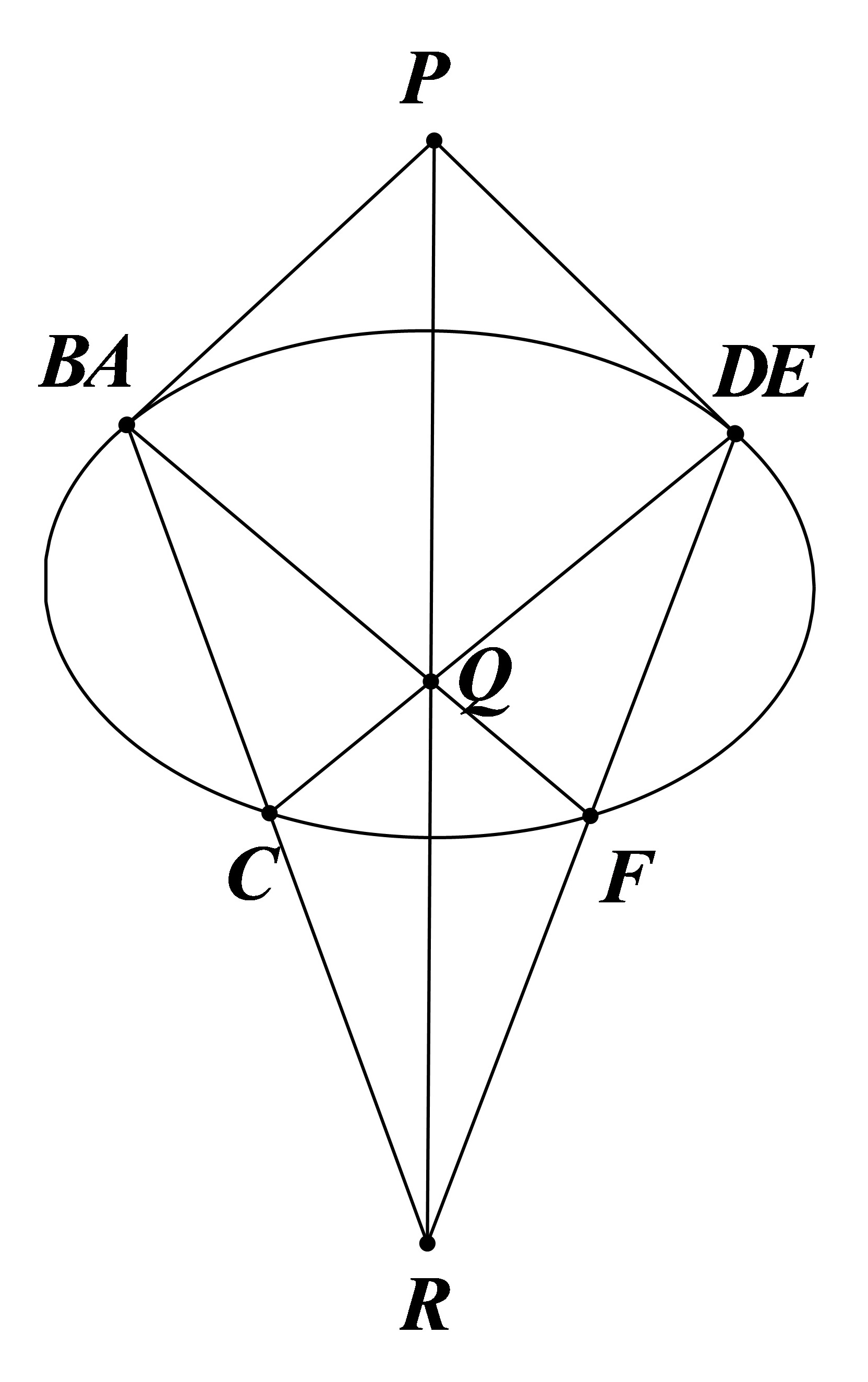
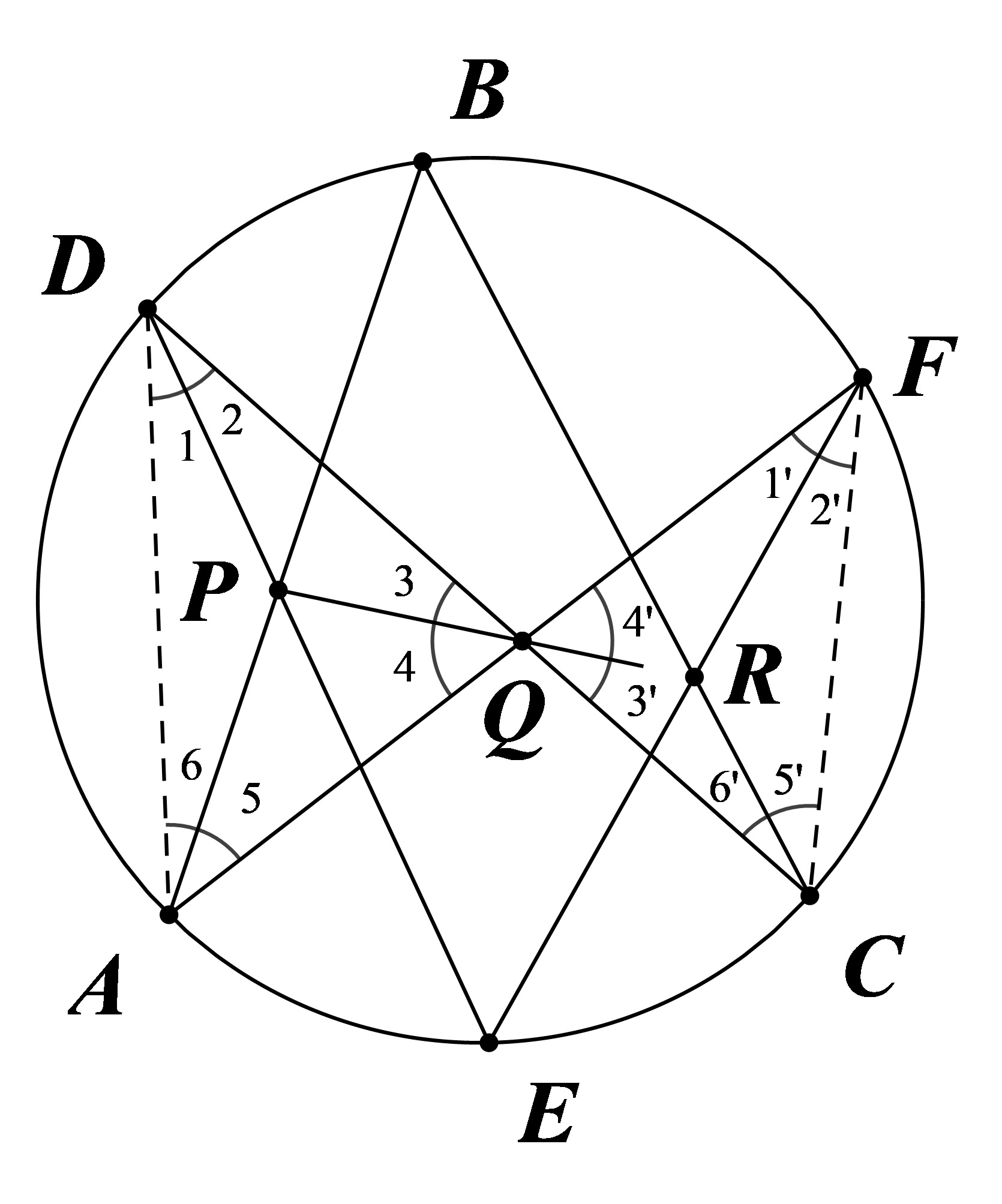
结合前两图得:椭圆任意内接四边形(如下图)有
其中
由
故
同理得

证毕。
例
例 1
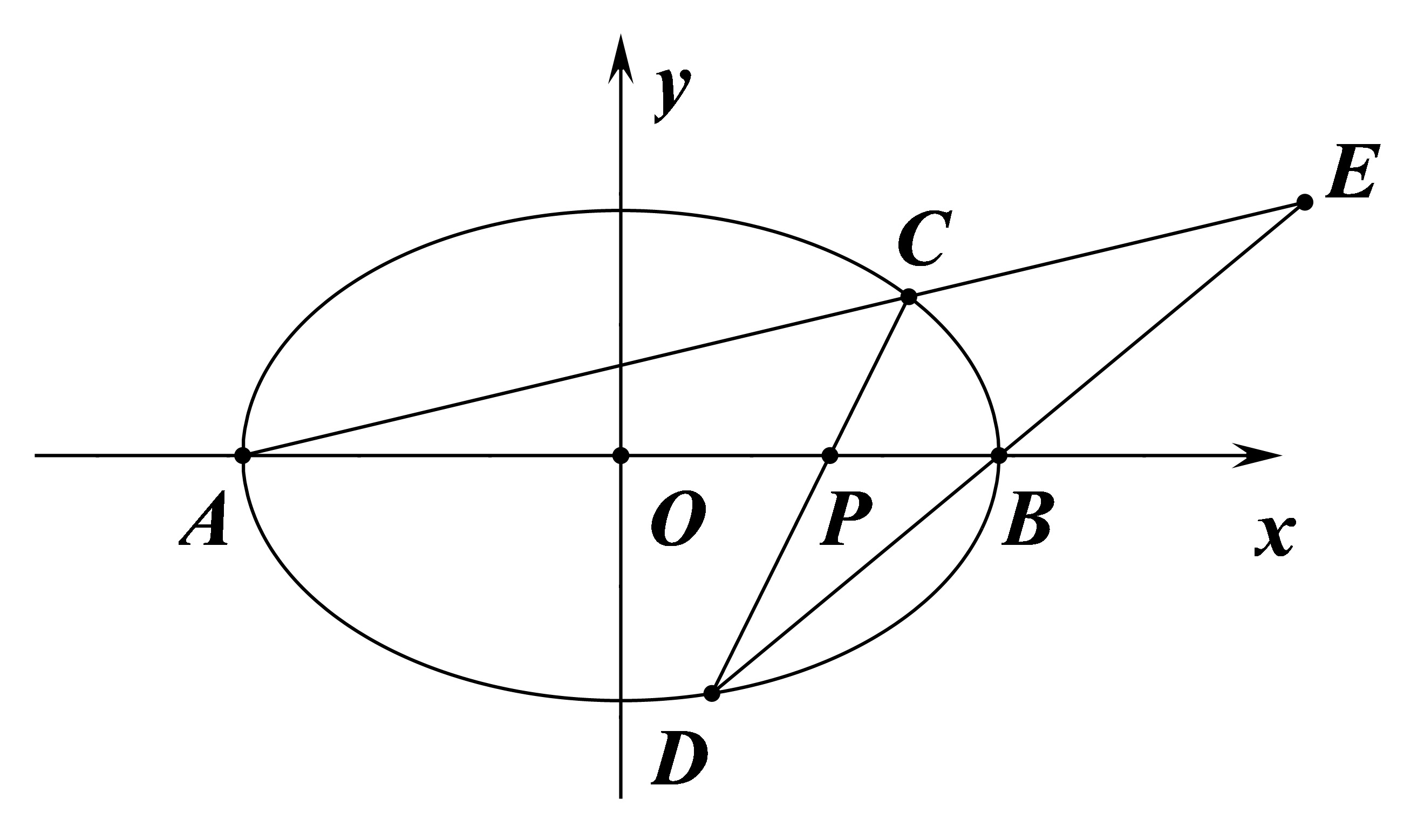
例 2
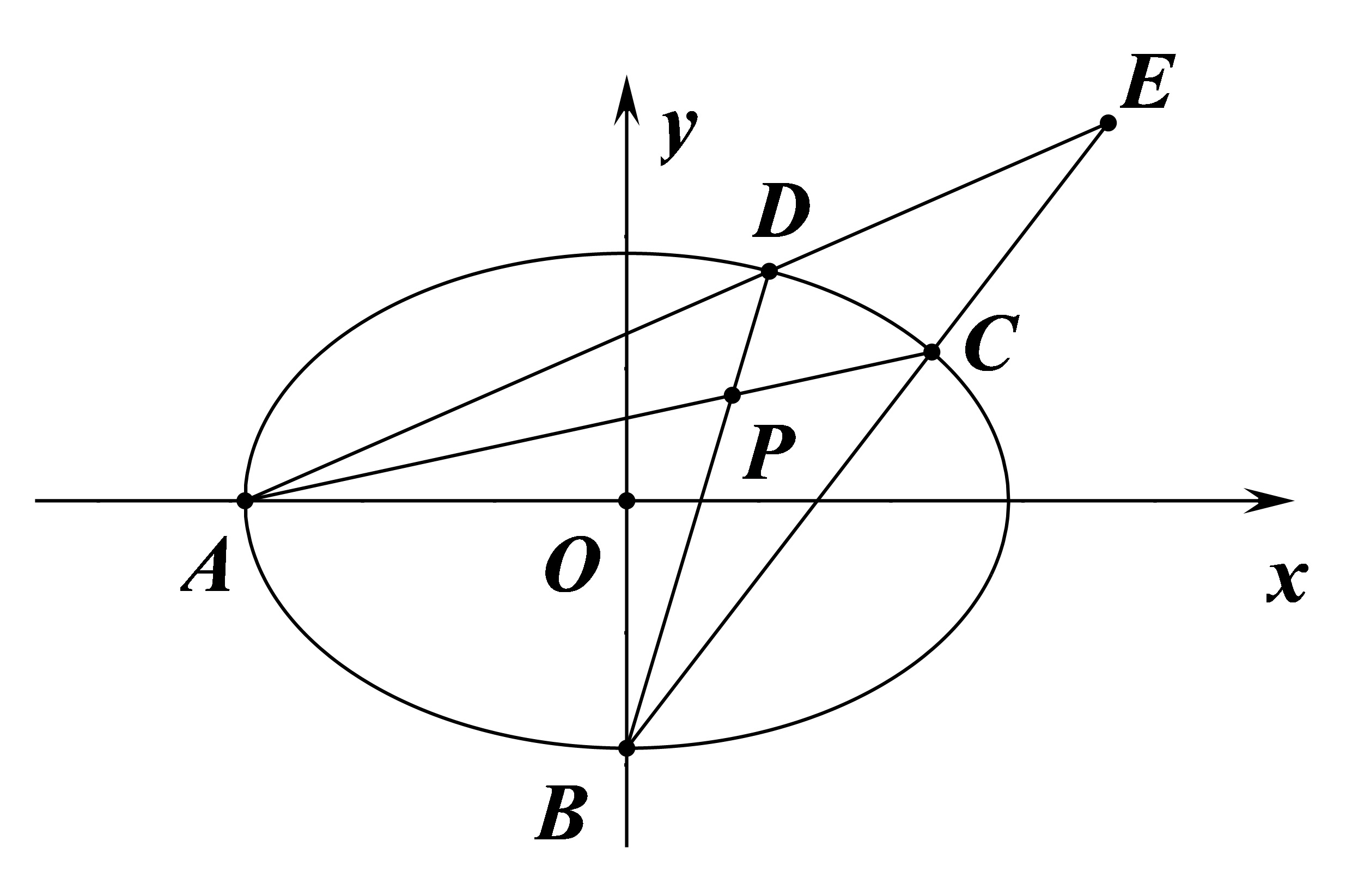
例 3
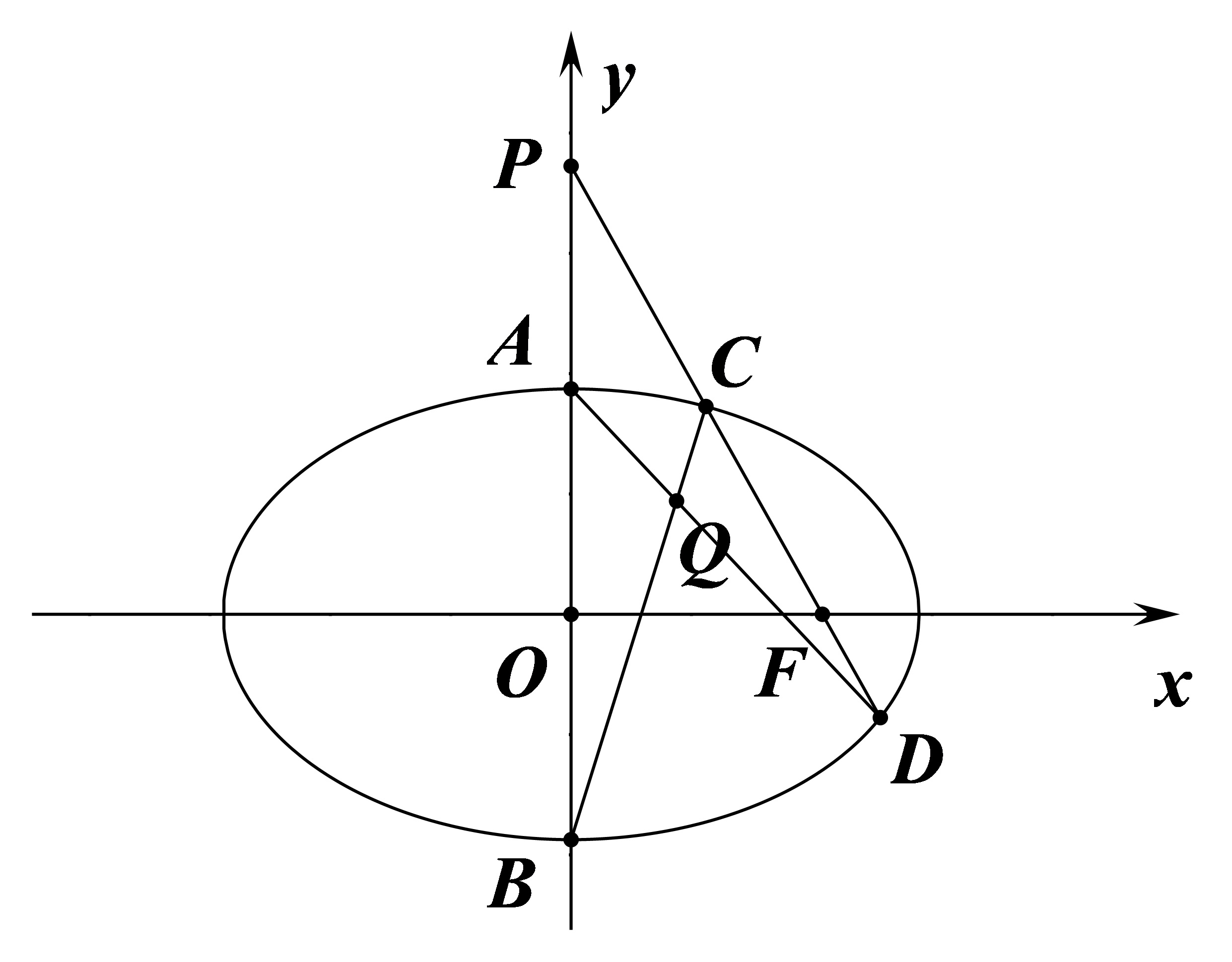
设
故