快速傅里叶变换（FFT）

快速傅里叶变换能在 $O(n\log{n})$ 的时间复杂度下计算两个 $n$ 次多项式的乘法。

对于 $n-1$ 次多项式

$$A(x)=a_0+a_1x+a_2x^2+\cdots+a_{n-1}x^{n-1}$$

系数表示法用 $n$ 个系数表示它。

$$\{a_0,a_1,\cdots,a_{n-1}\}$$

两点确定 $kx+b$，三点确定 $ax^2+bx+c$。以此类推，至少 $n$ 点才能确定 $n-1$ 次多项式。

点值表示法用至少 $n$ 个不同的点表示 $n-1$ 次多项式。

$$\{(x_0,y_0),(x_1,y_1),\cdots,(x_{n-1},y_{n-1})\}$$

离散傅里叶变换（Discrete Fourier Transform，DFT）是将多项式从 系数表示法 转换为 点值表示法 的算法，IDFT 是 DFT 的逆过程。

运用 DFT 和 IDFT 计算多项式乘法 $A(x)\cdot B(x)=C(x)$ 的主要步骤：

1. 对 $A(x)$ 和 $B(x)$ 使用 DFT，得到两个点集：

   $$\left\{\big(x_i,A(x_i)\big)\mid 0\le i< N\right\} \\ \left\{\big(x_i,B(x_i)\big)\mid 0\le i< N\right\}$$

2. 计算出 $C(x)$ 的点值表示法：

   $$\left\{\big(x_i,A(x_i)\cdot B(x_i)\big)\mid 0\le i< N\right\}$$

3. 使用 IDFT 将其转化为系数表示法。

其中 $N\ge C(x) \ 的次数 \ +1=A(x) \ 的次数 \ + B(x) \ 的次数 \ +1$，否则第二步得到的点太少，不足以确定最终的答案。

一般的 DFT 和 IDFT 时间复杂度高达 $O(n^2)$，而快速傅里叶变换（Fast Fourier Transform，FFT）可以把这个过程优化到 $O(n\log{n})$。

让我们从一个例子入手，先熟悉一下 $O(n^2)$ 的普通算法是什么样的。

现在我们来计算 $A(x)=x^2+x+1$ 和 $B(x)=x^2-3$ 的乘积 $C(x)$。

这个乘法的结果肯定是一个 $4$ 次的多项式，这意味着我们至少要取 $5$ 个点，那么就随便取 $x=1,2,3,4,5$ 好了。

第一步：计算 $A(x)$ 和 $B(x)$ 的点值表示法：

$$A(x)\longrightarrow\{(1,3),(2,7),(3,13),(4,21),(5,31)\}\\ B(x)\longrightarrow\{(1,-2),(2,1),(3,6),(4,13),(5,22)\}$$

第二步：计算 $C(x)=A(x)\cdot B(x)$ 的点值表示法：

$$C(x)\longrightarrow\{(1,-6),(2,7),(3,78),(4,273),(5,682)\}$$

第三步：转化为系数表示法。这一步的方法有很多，可以使用拉格朗日插值法等。总之最后算出来的结果是

$$C(x)=x^4 + x^3 - 2x^2 - 3x - 3$$

当 $C(x)$ 是 $n-1$ 次多项式时，需要取 $n$ 个不同的 $x$。其中每次计算 $A(x)\cdot B(x)$ 的时间复杂度为 $O(n)$，并且这个过程要重复 $n$ 次，那么总的时间复杂度为 $O(n^2)$。

上述流程存在一个比较现实的问题：在实际的应用场景中，多项式的次数往往很大。如果我们随意地取 $x$ 的值，计算出的 $A(x)$ 可能会超出基本变量类型的范围，那么这个算法很有可能在第一步就会搁浅。

所以 $x$ 的取值其实很有门道。它既不能让 $A(x)$ 太大，让计算机存不下；也不能让 $|A(x)|$ 太小，导致计算过程中发生精度的损失。这么看来，似乎只有 $0$，$1$ 和 $-1$ 这三个数比较合适。

但是只有这三个数是远远不够的。去哪里找其它的数呢？

这样的数，数学家们在复数域中找到了无穷多个。

如图 1，在复平面上画一个半径为 $1$ 的单位圆。圆上的每一点 $(\cos\theta,\sin\theta)$ 都可以表示复数 $\cos{\theta}+i\sin{\theta}$，其中 $\theta$ 是幅角，即它和原点的连线与实轴正半轴的夹角。

如果把圆周角 $N$ 等分，也就是令 $\theta=\frac{2\pi}{N}$，那么这个复数就被称作 单位复根，记作 $\omega_N$。

$$\omega_N=\cos\frac{2\pi}{N}+i\sin\frac{2\pi}{N}$$

中学课本告诉了我们复数乘法的规律：幅角相加模相乘。我们知道 $\omega_N$ 的模为 $1$，那么 $\omega_N^k$ 的模也就还是 $1$，且其幅角从原来的 $\frac{2\pi}{N}$ 变成了 $\frac{2k\pi}{N}$。

根据上述规律，不难发现，$\omega_N^0,\omega_N^1,\omega_N^2,\cdots,\omega_N^{N-1}$ 在单位圆上的分布是均匀的。图 2 展示了 $N=8$ 时的情况。

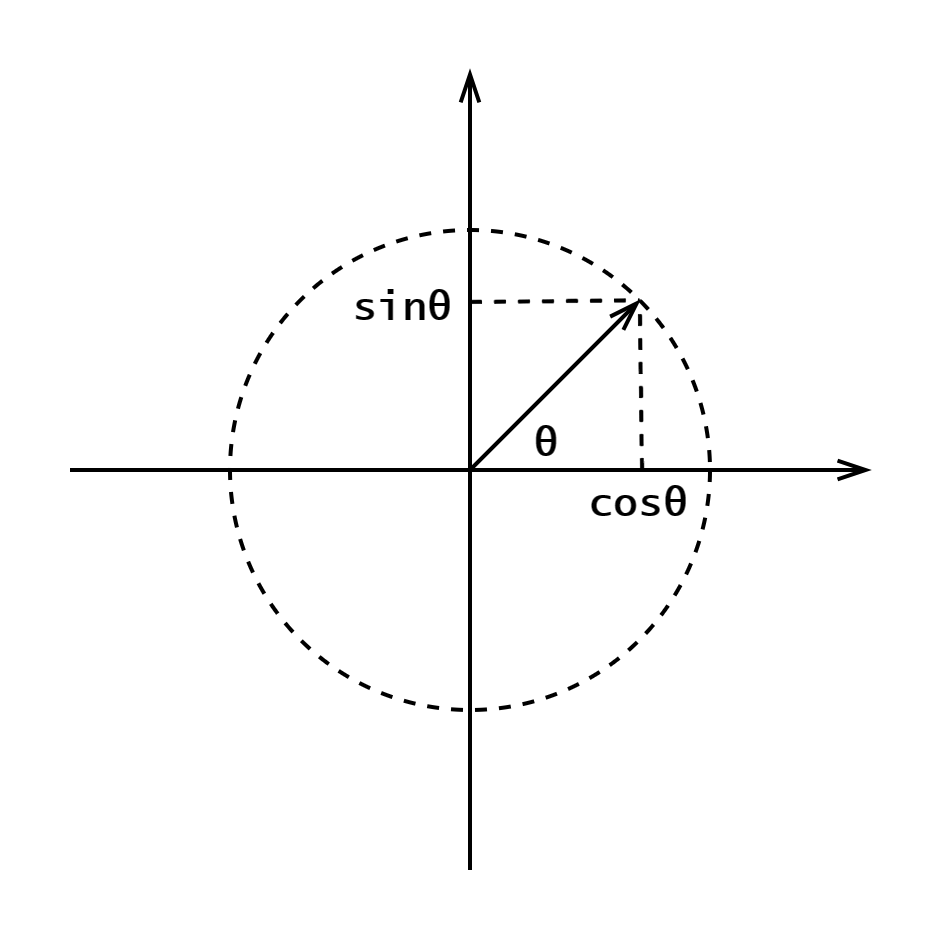图 1

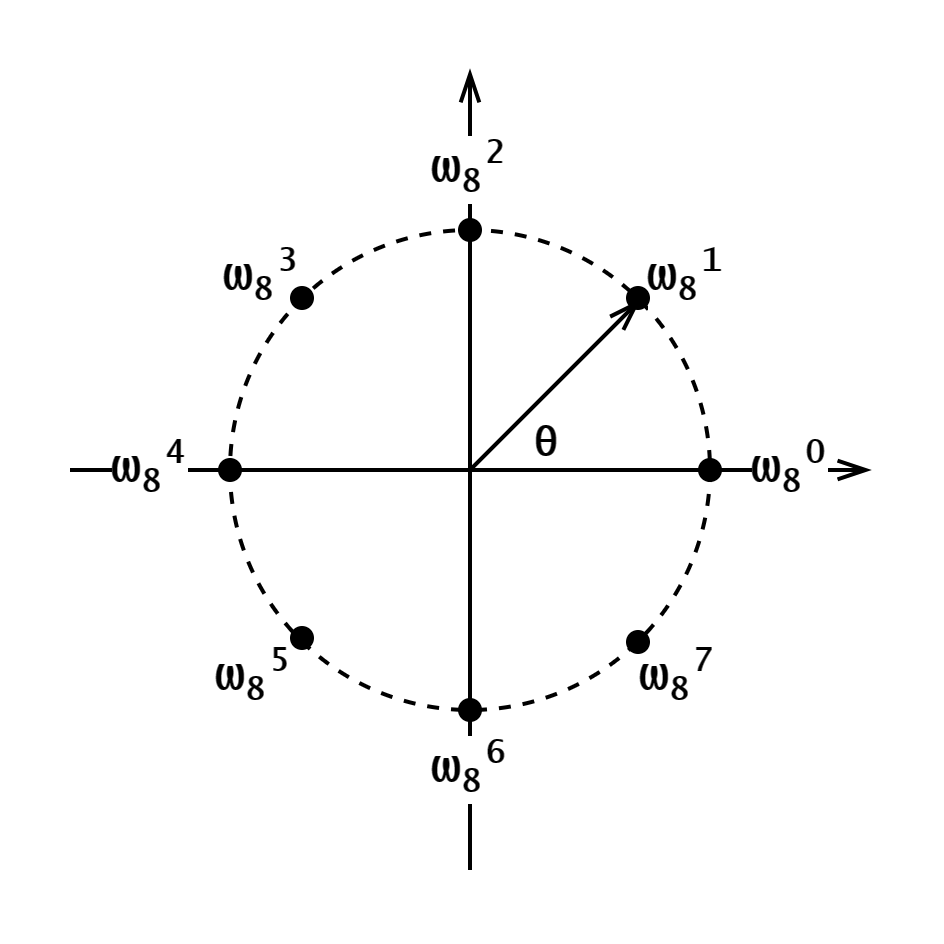图 2

单位复根还具有如下优异的性质：

1. 周期性：$\omega_N^N=1$
2. 消去性：$\omega_{2N}^{2k}=\omega_N^k$
3. 对称性：$\omega_N^{k+\frac{N}{2}}=-\omega_N^k$

证明并不困难。一方面可以用上文中 $\omega_N^k$ 的图像性质去推理；另一方面，直接套用欧拉公式

$$e^{\large i\theta}=\cos{\theta}+i\sin{\theta}\intro\omega_N=e^{\large\frac{2\pi}{N}i}$$

也能能轻易得证。

单位复根 恰好可以完美地解决 DFT 中取点的问题。代入 $x=\omega_N^k$ 既不会使 $y=A(x)$ 大到溢出，也不会使其小到失真，唯一别扭的地方就是 $x$ 和 $y$ 都是复数值。不过大部分编程语言都有支持复数运算的库，所以这不是大问题。因此当我们需要在 DFT 中取 $N$ 个点时，不妨就取

$$x=\omega_N^0,\omega_N^1,\omega_N^2,\cdots,\omega_N^{N-1}$$

但是单位复根仅仅是解决了计算过程中的问题。目前为止，这个算法的时间复杂度仍然是 $O(n^2)$。真正使其成为「快速」傅里叶变换的，是接下来要讲的「多项式分治」。

对一个 $n$ 项的多项式

$$A(x)=a_0+a_1x+a_2x^2+a_3x^3+\cdots+a_{n-2}x^{n-2}+a_{n-1}x^{n-1}$$

进行如下变换（假定 $n=2^k,k\in\mathbb{Z}$）：

1. 将偶数项留在前面，将奇数项移到后面（项数从 $0$ 开始计）

$$A(x)=a_0+a_2x^2+\cdots+a_{n-2}x^{n-2}+a_1x+a_3x^3+\cdots+a_{n-1}x^{n-1}$$

2. 对后一半提取公因式 $x$

$$A(x)=a_0+a_2x^2+\cdots+a_{n-2}x^{n-2}+x\cdot\left(a_1+a_3x^2+\cdots+a_{n-1}x^{n-2}\right)$$

设

$$A_\text{even}(x)=a_0+a_2x+\cdots+a_{n-2}x^{\frac{n}{2}-1}$$

$$A_\text{odd}(x)=a_1+a_3x+\cdots+a_{n-1}x^{\frac{n}{2}-1}$$

则

$$A(x)=A_\text{even}\left(x^2\right)+x\cdot A_\text{odd}\left(x^2\right)$$

注意这里我们将 $x^2$ 作为 $A_\text{even}$ 和 $A_\text{odd}$ 的变量。

将 $x=\omega_n^k$ 代入得：

$$\begin{aligned} A\left(\omega_n^k\right)&=A_\text{even}\left(\omega_n^{2k}\right)+\omega_n^k\cdot A_\text{odd}\left(\omega_n^{2k}\right)\newline &=\textcolor{red}{A_\text{even}\left(\omega_{n/2}^{k}\right)}+\omega_n^k\cdot \textcolor{blue}{A_\text{odd}\left(\omega_{n/2}^{k}\right)} \end{aligned}$$

将 $x=\omega_n^{k+n/2}=-\omega_n^k$ 代入得：

$$\begin{aligned} A\left(\omega_n^{k+n/2}\right)&=A\left(-\omega_n^k\right)\newline &=\textcolor{red}{A_\text{even}\left(\omega_{n/2}^{k}\right)}-\omega_n^k\cdot \textcolor{blue}{A_\text{odd}\left(\omega_{n/2}^{k}\right)} \end{aligned}$$

我们发现，$\textcolor{red}{A_\text{even}\left(\omega_{n/2}^{k}\right)}$ 和 $\textcolor{blue}{A_\text{odd}\left(\omega_{n/2}^{k}\right)}$ 各自又都是 $n/2$ 项多项式，它们也可以用同样的方法再往下拆分成更短的多项式之和。所以我们采用递归的方式去实现这个计算过程。

对每个 $A\left(\omega_n^k\right)$ 单独递归的效率太低。这里采用的递归策略是：先计算出

$$\left\{\textcolor{red}{A_\text{even}\left(\omega_{n/2}^0\right)},\textcolor{red}{A_\text{even}\left(\omega_{n/2}^1\right)},\cdots,\textcolor{red}{A_\text{even}\left(\omega_{n/2}^{n/2-1}\right)}\right\}$$

$$\left\{\textcolor{blue}{A_\text{odd}\left(\omega_{n/2}^0\right)},\textcolor{blue}{A_\text{odd}\left(\omega_{n/2}^1\right)},\cdots,\textcolor{blue}{A_\text{odd}\left(\omega_{n/2}^{n/2-1}\right)}\right\}$$

再根据之前推出的公式

$$\begin{cases} A\left(\omega_n^k\right)&=&\textcolor{red}{A_\text{even}\left(\omega_{n/2}^{k}\right)}&+&\omega_n^k\cdot \textcolor{blue}{A_\text{odd}\left(\omega_{n/2}^{k}\right)}\\ \\ A\left(\omega_n^{k+n/2}\right)&=&\textcolor{red}{A_\text{even}\left(\omega_{n/2}^{k}\right)}&-&\omega_n^k\cdot \textcolor{blue}{A_\text{odd}\left(\omega_{n/2}^{k}\right)} \end{cases} \quad k=0,1,\cdots,\frac{n}{2}-1$$

得出

$$\left\{A\left(\omega_{n}^0\right),A\left(\omega_{n}^1\right),\cdots,A\left(\omega_{n}^{n-1}\right)\right\}$$

进而得出我们所需要的 $n$ 个点值。

设 $a=\{a_0,a_1,\cdots,a_{n-1}\}$ 是存放 $A(x)$ 系数的数组，函数 $\text{DFT}(a)$ 的功能是算出并返回

$$\left\{A\left(\omega_{n}^0\right),A\left(\omega_{n}^1\right),\cdots,A\left(\omega_{n}^{n-1}\right)\right\}$$

以下是 $\text{DFT}(a)$ 的伪代码：

$$\DeclareMathOperator{\let}{let \ } \DeclareMathOperator{\if}{If \ } \DeclareMathOperator{\for}{For \ } \DeclareMathOperator{\return}{return \ } \begin{aligned} &\text{DFT}(a):\newline &\qquad n:=a.\text{size}()\newline &\qquad \if \ n=1:\newline &\qquad \qquad \text{return} \ a\newline &\qquad y^\text{even}:=\text{DFT}(\{a_0,a_2,\cdots,a_{n-2}\})\newline &\qquad y^\text{odd} \ :=\text{DFT}(\{a_1,a_3,\cdots,a_{n-1}\})\newline &\qquad y:=\{\}\newline &\qquad \omega:=1 \newline &\qquad \textstyle \omega_n:=\cos\frac{2\pi}{n}+i\sin\frac{2\pi}{n}\newline &\qquad \for \ \textstyle k = 0 \cdots \frac{n}{2}-1:\newline &\qquad \qquad y_k=y^\text{even}_k+\omega * y^\text{odd}_k\newline &\qquad \qquad y_{k+\frac{n}{2}}=y^\text{even}_k-\omega * y^\text{odd}_k\newline &\qquad \qquad \omega=\omega*\omega_n\newline &\qquad \return y \end{aligned}$$

可以画出 $\text{DFT}$ 算法的递归图：

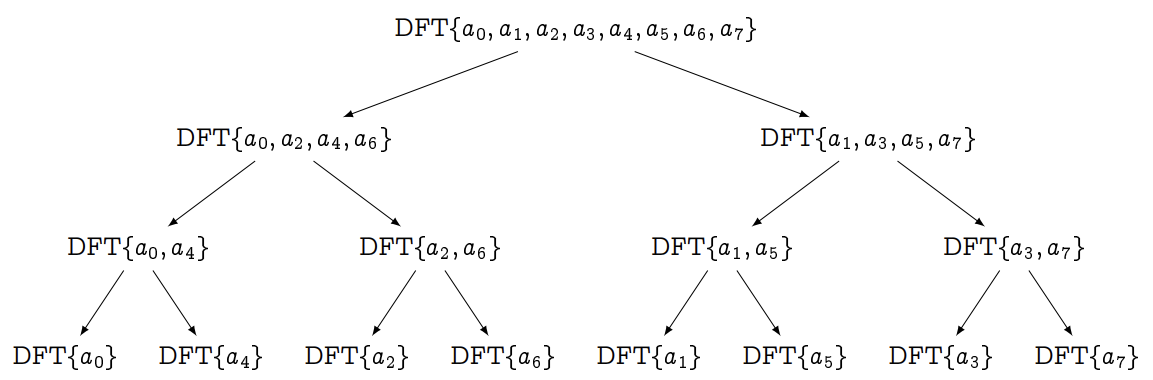容易看出，以上分治算法每次都能递归地将规模为 $n$ 的问题拆分成两个规模为 $n/2$ 的问题，总时间复杂度为 $O(n\log{n})$。

之所以在一开始假定 $n=2^k,k\in\mathbb{Z}$，就是为了确保每次对多项式进行拆分时都能恰好平均分为两半。如果多项式的项数 $n$ 不符合这个要求，那么我们可以往后面补 $0$ 项，直到达成这个要求。

例如对于 $A(x)=1+x+4x^2+5x^3+x^4+4x^5$ 一共只有 $6$ 项，还差 $2$ 项就能符合要求，所以往后面补两个 $0$ 项：

$$A(x)=1+x+4x^2+5x^3+x^4+4x^5+0x^6+0x^7$$

以上就是 FFT 加速算法的全部内容。不过我们只是用它加速了 DFT 的过程。多项式乘法的最后一步，也就是 IDFT，我们仍然没有提及。实际上 IDFT 也可以用同样的算法进行加速。

前文所论述的 DFT 算法实际上是在解以下方程组：

$$\begin{cases} a_0 & + & a_1 & + & a_2 & + & \cdots & + & a_{n-1} & = & y_0\newline a_0 & + & a_1\left(\omega_n\right) & + & a_2\left(\omega_n\right)^2 & + & \cdots & + & a_{n-1}\left(\omega_n\right)^{n-1} & = & y_1\newline a_0 & + & a_1\left(\omega_n^2\right) & + & a_2\left(\omega_n^2\right)^2 & + & \cdots & + & a_{n-1}\left(\omega_n^2\right)^{n-1} & = & y_2\newline & & & & & &\cdots\newline a_0 & + & a_1\left(\omega_n^{n-1}\right) & + & a_2\left(\omega_n^{n-1}\right)^2 & + & \cdots & + & a_{n-1}\left(\omega_n^{n-1}\right)^{n-1} & = & y_{n-1} \end{cases}$$

令 $\mathbf{A}=\begin{pmatrix}a_0 \newline a_1 \newline a_2 \newline\vdots \newline a_{n-1}\end{pmatrix}$，$\mathbf{Y}=\begin{pmatrix}y_0 \newline y_1 \newline y_2 \newline \vdots \newline y_{n-1}\end{pmatrix}$，则上述方程组可以写成矩阵乘法的形式：

$$\begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \newline 1 & \omega_n & \left(\omega_n\right)^2 & \cdots & \left(\omega_n\right)^{n-1} \newline 1 & \omega_n^2 & \left(\omega_n^2\right)^2 & \cdots & \left(\omega_n^2\right)^{n-1} \newline \vdots & \vdots & \vdots & \ddots & \vdots \newline 1 & \omega_n^{n-1} & \left(\omega_n^{n-1}\right)^2 & \cdots & \left(\omega_n^{n-1}\right)^{n-1} \newline \end{pmatrix} \cdot \mathbf{A} = \mathbf{Y}$$

DFT 的数学本质就是已知 $\mathbf{A}$，求解 $\mathbf{Y}$。而 IDFT 作为其逆过程，实际上就是已知 $\mathbf{Y}$，求解 $\mathbf{A}$。这正好对应了从点值表示法向系数表示法的转换。

为了实现 IDFT，我们可以很自然地对上式做出以下变换：

$$\mathbf{A} = \begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \newline 1 & \omega_n & \left(\omega_n\right)^2 & \cdots & \left(\omega_n\right)^{n-1} \newline 1 & \omega_n^2 & \left(\omega_n^2\right)^2 & \cdots & \left(\omega_n^2\right)^{n-1} \newline \vdots & \vdots & \vdots & \ddots & \vdots \newline 1 & \omega_n^{n-1} & \left(\omega_n^{n-1}\right)^2 & \cdots & \left(\omega_n^{n-1}\right)^{n-1} \newline \end{pmatrix}^{-1} \cdot \mathbf{Y}$$

那怎么求中间的这个逆矩阵呢？我们一眼就可以盯真出这是个特殊范德蒙矩阵的逆矩阵。

再结合 单位复根 的性质就可以得出

$$\begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \newline 1 & \omega_n & \left(\omega_n\right)^2 & \cdots & \left(\omega_n\right)^{n-1} \newline 1 & \omega_n^2 & \left(\omega_n^2\right)^2 & \cdots & \left(\omega_n^2\right)^{n-1} \newline \vdots & \vdots & \vdots & \ddots & \vdots \newline 1 & \omega_n^{n-1} & \left(\omega_n^{n-1}\right)^2 & \cdots & \left(\omega_n^{n-1}\right)^{n-1} \newline \end{pmatrix}^{-1} = \frac{1}{n} \begin{pmatrix} 1 & 1 & 1 & \cdots & 1 \newline 1 & \omega_n^{-1} & \left(\omega_n^{-1}\right)^2 & \cdots & \left(\omega_n^{-1}\right)^{n-1} \newline 1 & \omega_n^{-2} & \left(\omega_n^{-2}\right)^2 & \cdots & \left(\omega_n^{-2}\right)^{n-1} \newline \vdots & \vdots & \vdots & \ddots & \vdots \newline 1 & \omega_n^{-(n-1)} & \left(\omega_n^{-(n-1)}\right)^2 & \cdots & \left(\omega_n^{-(n-1)}\right)^{n-1} \newline \end{pmatrix}$$

再将这个结果代入进去，并还原成方程组：

$$\begin{cases} y_0 & + & y_1 & + & y_2 & + & \cdots & + & y_{n-1} & = & n\cdot a_0\newline y_0 & + & y_1\left(\omega_n^{-1}\right) & + & y_2\left(\omega_n^{-1}\right)^2 & + & \cdots & + & y_{n-1}\left(\omega_n^{-1}\right)^{n-1} & = & n\cdot a_1\newline y_0 & + & y_1\left(\omega_n^{-2}\right) & + & y_2\left(\omega_n^{-2}\right)^2 & + & \cdots & + & y_{n-1}\left(\omega_n^{-2}\right)^{n-1} & = & n\cdot a_2\newline & & & & & &\cdots\newline y_0 & + & y_1\left(\omega_n^{-(n-1)}\right) & + & y_2\left(\omega_n^{-(n-1)}\right)^2 & + & \cdots & + & y_{-(n-1)}\left(\omega_n^{-(n-1)}\right)^{n-1} & = & n\cdot a_{n-1} \end{cases}$$

这个方程组和原先的方程组极为相似。这意味着我们只需调整 DFT 代码中某些参数的正负号，并且将最终的结果除以 $n$，就能得到 IDFT 的代码。