快速傅里叶变换：蝶形优化

能看出蝶形的受上赏。

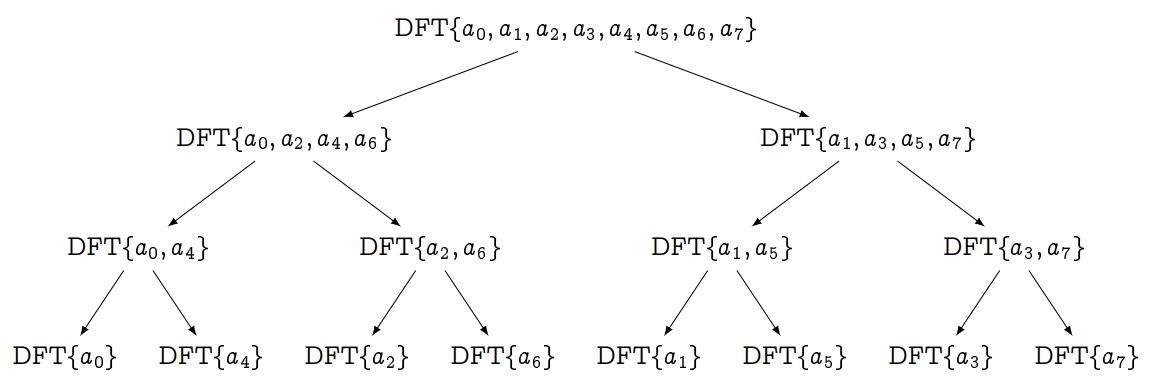
在快速傅里叶变换 (FFT)中，$\text{FFT}$ 算法使用分治思想，每次都将系数数组 $\{a_0,\cdots,a_7\}$ 按元素位置的奇偶性拆分成两半，并使用递归的方法，自上而下地进行运算。

每次拆分时，都要把偶数项拷贝到新数组 $A_\text{even}$，把奇数项拷贝到新数组 $A_\text{odd}$，再执行运算 $\text{DFT}\left(A_\text{even}\right)$ 和 $\text{DFT}\left(A_\text{odd}\right)$。这么做既费时又费力。

如果我们一开始就将 $a_0\sim a_7$ 的顺序处理成

$$\{a_0,a_4,a_2,a_6,a_1,a_5,a_3,a_7\}$$

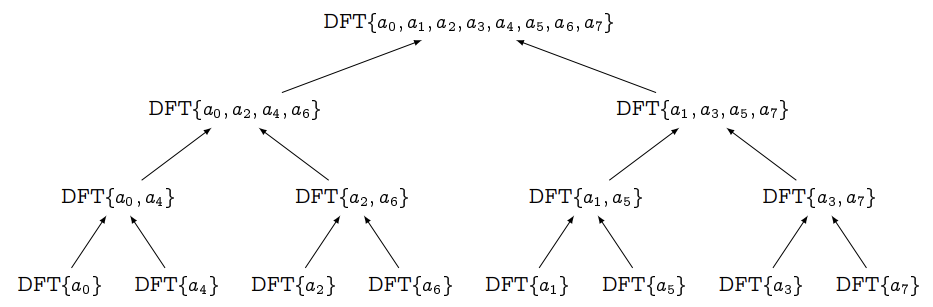
并自下而上地进行运算

这样就能避免愚蠢的拷贝操作，进一步压榨计算机的算力。

这个优化过程被称为蝶形优化。

蝶形优化 #

简言之，我们需要的是这样的变换：

$$\begin{aligned} 0&\longrightarrow 0 \\ 0,1&\longrightarrow 0,1 \\ 0,1,2,3&\longrightarrow 0,2,1,3 \\ 0,1,2,3,4,5,6,7&\longrightarrow 0,4,2,6,1,5,3,7\\ & \ \cdots \end{aligned}$$

这个变换的策略出人意料地简单：将每个数转为二进制（在最高位补零补到一样长），然后反转它们，就能得到蝶形优化的结果。

举个例子：

$x \ \text{Decimal}$	$x \ \text{Binary}$	$y \ \text{Bit-Reverse}$	$y \ \text{Decimal}$
$0$	$000$	$000$	$0$
$1$	$001$	$100$	$4$
$2$	$010$	$010$	$2$
$3$	$011$	$110$	$6$
$4$	$100$	$001$	$1$
$5$	$101$	$101$	$5$
$6$	$110$	$011$	$3$
$7$	$111$	$111$	$7$

是不是很神奇。

如果你对该策略仍持有怀疑态度，仍然不能心安理得地直接使用蝶形优化算法，那么我们浅浅地证明一下好了。

证明 #

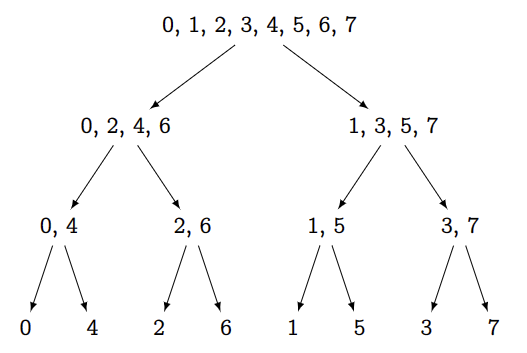
我们仅保留数组 $a$ 的下标，略去其它部分，重新画出 $\text{FFT}$ 的递归图。

这张图所展示的递归策略可以被简要地概括为：

info

在每一层，如果数 $k$（在其序列中）在偶位，就把它划分到左侧；否则数 $k$ 在奇位，就把它划分到右侧。

warning

需要特别强调「在其序列中」这个点。例如在第二层 $$0,2,4,6,\quad 1,3,5,7$$ 其中数字 $5$ 的位置应该是 $3$ 而不是 $7$。因为 $5$ 所在的序列是 $1,3,5,7$，而不是一整排。

问题来了：在某一层，如何判断数 $k$ 是处于偶位，还是处于奇位？

首先我们需要归纳 $k$ 在每一层的位置。

note

容易看出：

在第一层：数 $k$ 排在第 $k$ 位
在第二层：数 $k$ 排在第 $\lfloor k\div2\rfloor$ 位
在第三层：数 $k$ 排在第 $\lfloor k\div2^2\rfloor$ 位
…
在第 $n$ 层，数 $k$ 排在第 $\lfloor k\div2^{n-1}\rfloor$ 位。

我们直接将 $\lfloor k\div2^{n-1}\rfloor$ 对 $2$ 取模，若得到 $0$，说明这个位置是个偶数，也就是 $k$ 在偶位；相反地，若得到 $1$，则说明 $k$ 在奇位。

可能有人已经发现了

$$\lfloor k\div2^{n-1}\rfloor\bmod 2$$

这个式子就是 $k$ 在二进制下的第 $n$ 位的数字。

也就是说，我们只需要判断 $k$ 的二进制第 $n$ 位，就能知道 $k$ 在第 $n$ 层是处于偶位，还是处于奇位。

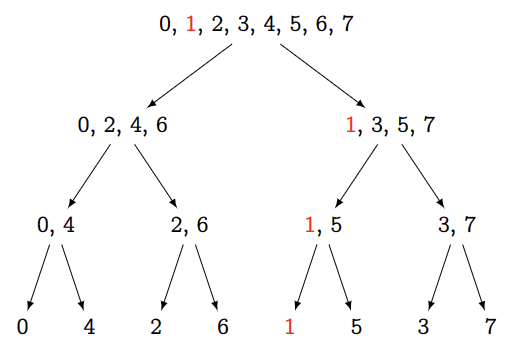
考察数字 $1=(001)_2$ 从上到下的位置变化：

在第一层，$(001)_2$ 的第一位是 $1$，说明它在奇位，因此被划分到右侧
在第二层，$(001)_2$ 的第二位是 $0$，说明它在偶位，因此被划分到左侧
在第三层，$(001)_2$ 的第三位是 $0$，说明它在偶位，因此被划分到左侧

现在，思考一个问题：数 $k$ 在第一层被划分到右侧，意味着什么？——意味着它最终肯定处于后 $50\%$ 的地方。可以认为，变换后数 $k$ 的位序的二进制最高位是 $1$。

$$000\quad001\quad010\quad011\quad\overset{\large 后 \ 50\%}{\overbrace{100\quad101\quad110\quad111}}$$

note

进一步地，我们可以归纳出：

在第一层
- 被划分到左侧 $\Rightarrow$ 最高位为 $0$
- 被划分到右侧 $\Rightarrow$ 最高位为 $1$
在第二层
- 被划分到左侧 $\Rightarrow$ 次高位为 $0$
- 被划分到右侧 $\Rightarrow$ 次高位为 $1$
…

现在重新审视数字 $1=(001)_2$ 的位置变化：

在第一层，$(001)_2$ 的第一位是 $1$，被划分到右侧，变换后它的位序的最高位是 $1$
在第二层，$(001)_2$ 的第二位是 $0$，被划分到左侧，变换后它的位序的次高位是 $0$
在第三层，$(001)_2$ 的第三位是 $0$，被划分到左侧，变换后它的位序的第三高位是 $0$

即 $1=(001)_2$ 变换后的位序是 $(100)_2=4$，而这个 $100$ 就是 $001$ 反转的结果。

同理，$4=(100)_2$ 变换后的位序是 $(001)_2=1$。因此可以认为，变换后 $4$ 和 $1$ 发生了交换。也就是，原先是 $1$ 的地方，变换后成了 $4$；原先是 $4$ 的地方，变换后成了 $1$。

那么，原先是 $k$ 的地方，变换后成了 $k$ 的二进制反转。

证毕。

模板 #

#include <bits/stdc++.h>

using namespace std;

const double PI = acos(-1);
typedef complex<double> Comp;

int reverseBits(int n, int log2n) {
    int reversed = 0;
    for (int i = 0; i < log2n; i++) {
        if (n & (1 << i)) {
            reversed |= 1 << (log2n - 1 - i);
        }
    }
    return reversed;
}

void bit_reverse_swap(vector<Comp>& a) {
    int n = a.size();
    int log2n = 0;

    while ((1 << log2n) < n) log2n++;

    for (int i = 0; i < n; i++) {
        int reversed = reverseBits(i, log2n);
        if (i < reversed) {
            swap(a[i], a[reversed]);
        }
    }
}

void FFT(vector<Comp>& a, bool invert) {
    int n = a.size();
    bit_reverse_swap(a);

    for (int len = 2; len <= n; len <<= 1) {
        double theta = 2 * PI / len * (invert ? -1 : 1);
        Comp wn(cos(theta), sin(theta));
        for (int i = 0; i < n; i += len) {
            Comp w(1);
            for (int j = 0; j < len / 2; ++j) {
                Comp u = a[i + j];
                Comp v = a[i + j + len / 2] * w;
                a[i + j] = u + v;
                a[i + j + len / 2] = u - v;
                w *= wn;
            }
        }
    }
    if (invert) {
        for (Comp& x : a) 
            x /= n;
    }
}

vector<Comp> multiply(vector<Comp> A, vector<Comp> B) {
    int n = 1;
    while (n < A.size() + B.size()) 
        n *= 2;
    A.resize(n);
    B.resize(n);

    FFT(A, false);
    FFT(B, false);
    
    vector<Comp> C(n);
    for (int i = 0; i < n; i++)
        C[i] = A[i] * B[i];
    
    FFT(C, true);

    for (int i = 0; i < n; i ++)
        C[i] = round(C[i].real());

    while (C.size() && ! C.back().real())
        C.pop_back();

    return C;
}

int main() {
    vector<Comp> A = {1, 2, 3}; // Represents the polynomial 1 + 2x + 3x^2
    vector<Comp> B = {4, 5};    // Represents the polynomial 4 + 5x
    
    vector<Comp> C = multiply(A, B);
    
    for (auto i : C)
        cout << i.real() << ' ';
    cout << endl;
    
    return 0;
}